Na manhã de segunda-feira, seu amigo Jorge se aproxima de você e diz: “Estou pensando em um número entre 1 e 100”. Como bom esportista, você entra no jogo e arrisca 43. “Não, muito baixo!”, declara Jorge. “Então, que tal 82?”, pergunta você. “Muito alto!”, responde Jorge. Você continua tentando adivinhar. 60 é baixo demais. 76 é muito alto. 70 é muito baixo. Satisfeito por estar se aproximando, você pergunta: “Que tal 75?” “É isso aí!”, exclama Jorge, enquanto você marcha triunfalmente para sua primeira aula do dia. 

Mas, depois da aula, você se depara novamente com Jorge, que aparentemente está pensando em maneiras de confundi-lo: por que se limitar a números positivos? Por que não tentar também com números negativos? “Agora, estou pensando em um número entre 100 negativo e 100”, anuncia Jorge, alegremente. Você decide morder a isca e rapidamente descobre que isso não muda muito o jogo. Vai dando palpites e, subindo e descendo, fica cada vez mais perto do alvo. Se o número de Jorge é -32 e você já descobriu que -33 é baixo demais e -31 é alto demais, então sabe que a resposta é -32. Mas descobre uma coisa: não há nada de especial em -100 e 100! Se você começar com um número entre -1.000 e 1.000, acabará adivinhando o número correto, mesmo que precise de mais algumas tentativas. Marcha vitoriosamente para sua segunda aula, confiante em que estará preparado para o próximo desafio de Jorge. 

No entanto, durante essa aula, você percebe ter assumido que Jorge sempre escolherá um número inteiro. E se as frações forem permitidas? Suponha que Jorge escolha um número entre 0 e 1, por exemplo, 3/22. Você tem que chutar um número em algum lugar ao longo da sequência numérica de 0 a 1. Tenta começar exatamente no meio e chuta 1/2. Jorge diz que seu palpite é alto, então você sabe que a resposta está em algum lugar na sequência numérica entre 0 e 1/2. Você chuta no meio novamente: 1/4. Jorge diz que 1/4 ainda é alto, assim você sabe que a resposta deve estar na sequência numérica entre 0 e 1/4. Continuando com sua estratégia, você chuta 1/8, 3/16, 5/32, 9/64, … Uma representação desse jogo é mostrada na Figura 1. Parece que está demorando muito! Será que você vai chutar o número certo? Talvez fosse melhor mudar sua estratégia. Ou você está condenado a chutar para sempre? 

Uma nova estratégia: expansões decimais

Vamos olhar para esses números de uma maneira diferente e considerá-los como decimais. Podemos transformar uma fração em decimal dividindo o numerador pelo denominador. Veja como funciona para a fração 7/16: 

Para o primeiro passo da divisão, perguntamos quantos 16 existem em 70. (Na verdade, estamos perguntando quantos 1,6 há em 7,0, mas isso equivale a perguntar quantos 16 há em 70). Como 16 x 4 = 64, escrevemos um 4 acima do 0 em 7,0. Então subtraímos 64 de 70 e obtemos 6, que é chamado de resto. 

Para o próximo passo, tiramos o próximo 0 de 7,00. Então perguntamos quantos 16 existem em 60. Como 16 x 3 = 48, escrevemos um 3 acima do segundo 0. Depois, subtraímos 48 de 60 para obter um resto de 12. 

Continuamos esse processo, tirando zeros após cada resto e perguntando quantos 16 há no número resultante. Depois de fazer isso quatro vezes, obtemos um resto de 0, que contém nele zero 16. Nesse ponto, terminamos nossa divisão longa e podemos dizer que 7/16 = 0,4375. Se você estiver jogando o jogo de adivinhar o número, poderá chegar a essa versão decimal de 7/16 em várias etapas curtas. A tabela abaixo mostra uma possível maneira de fazer isso. O H significa que seu palpite foi muito alto e o L significa que seu palpite foi muito baixo. 

Como o decimal para o número 7/16 termina, você pode obter o número exato supondo um dígito por vez no decimal. Isso acontece com todas as frações? Vamos ver o decimal para 3/22. 

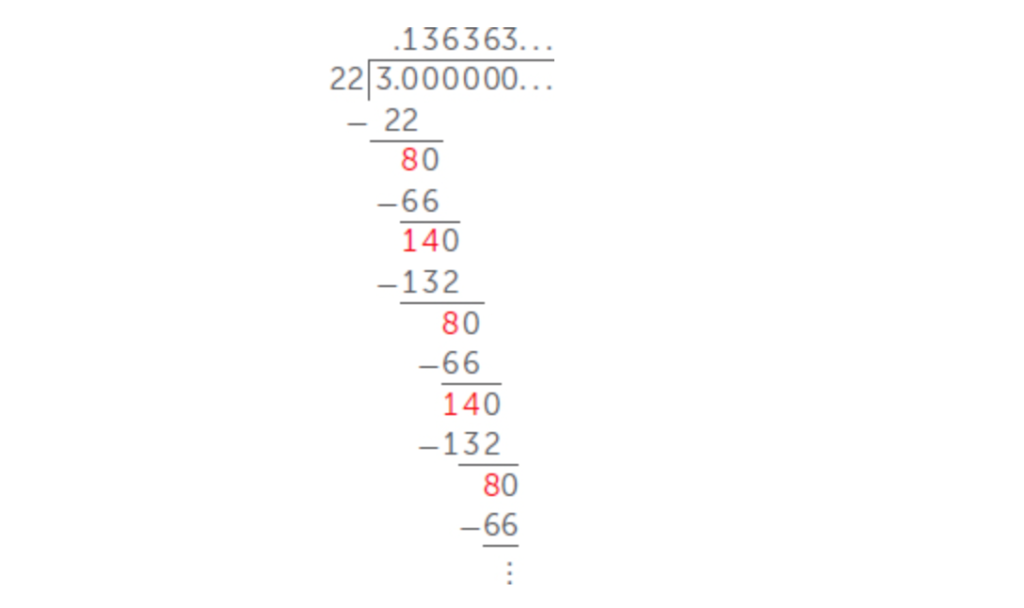
Seguindo o mesmo processo de divisão, obtemos 1 em cima com o resto 8, um 3 em cima com o resto 14, um 6 em cima com o resto 8, um 3 em cima com o resto 14 … Mas espere! Já vimos esses restos e sabemos que o próximo número no topo é um 6 com resto 14 novamente. À medida que continuamos a dividir, os dois restos repetidos 8 e 14 nos fornecem 3 e 6 repetidos na expansão decimal para 3/22. Isso significa que, se você tentar adivinhar o número 3/22 com uma casa decimal por vez, ficará tentando para sempre! 

Números racionais

Todos os números que consideramos até agora são chamados de números racionais. Um número racional é qualquer número que pode ser escrito como uma fração a/b de dois números inteiros (eles ou seus negativos), a e b. Isso significa que 2/5 é um número racional já que 2 e 5 são inteiros. Também 3 é um número racional, pois pode ser escrito como 3 = 3/1, e 4,5 é um número racional porque pode ser escrito como 4,5 = 9/2. Mesmo se não escrevemos 3 e 4,5 como frações, eles são números racionais porque podemos escrever uma fração igual a cada um deles. 

Vimos que alguns números racionais, como 7/16, têm expansões decimais que terminam. Nós chamamos esses números de decimais finais. Outros números racionais, como 3/22, têm expansões decimais que continuam indefinidamente. Mas sabemos que mesmo as expansões decimais que não terminam se repetem, então as chamamos de decimais repetitivos. 

Para qualquer número racional a/b, os únicos restos que podemos obter quando calculamos o decimal são os números 0, 1, 2, 3, …, b-2, b-1. Por exemplo, quando estávamos transformando 3/22 em um decimal, as únicas opções que tínhamos para os restos eram 0, 1, 2, 3, …, 20, 21. Uma vez que há somente um número finito de restos, os restos devem começar a se repetir a dada altura. Isso é correto para todas as frações cujos decimais não terminam. Mesmo que haja um padrão de repetição para os decimais para essas frações, nunca adivinharemos o número exato no jogo de adivinhação se estivermos sugerindo uma casa decimal por vez, porque o decimal continua para sempre – e não podemos citar dígitos infinitos! 

É possível ir na direção inversa e transformar decimais em frações também! Quando temos uma expansão decimal final, como 4,132, podemos mudar isso para uma fração usando o valor posicional. O 2 de 4,132 está na casa dos milésimos, então 4,132 = 4132/1000. Se estivermos começando com uma dízima periódica, teremos que trabalhar um pouco mais para encontrar sua fração correspondente. Considere, por exemplo, 0,353535… Chame-o de número A. A parte repetida 35 tem dois dígitos, então multiplicamos A por 100 para mover o decimal em duas casas. Isso dá 100A = 35,353535…. Observe que todas as casas decimais em A e em 100A coincidem. Subtraímos A de 100A para obter 99A. Quando subtraímos os decimais, o 0,353535… é o mesmo para ambos e é eliminado na diferença. Portanto, ficamos apenas com números inteiros! 

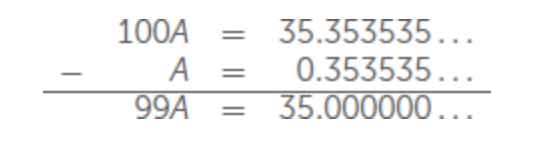
Temos 99A = 35; então, quando dividimos por 99, obtemos A = 35/99. Para qualquer dízima periódica, podemos usar o mesmo processo a fim de encontrar a fração correspondente. Multiplicamos por 10, 100, 1000 ou o que for necessário a fim de mover a vírgula o suficiente para que os dígitos decimais se alinhem. Depois, subtraímos e usamos o resultado para encontrar a fração correspondente. Isso significa que cada dízima periódica é um número racional! 

Números irracionais

E se tivermos uma expansão decimal que não termina, mas cujos dígitos não se repetem? Por exemplo, observe 0,101001000100001…. Nesse número, aumentamos a quantidade de 0s entre cada par de 1s, primeiro tendo um 0 intermediário, depois dois 0s, depois três 0s, etc. Esse não pode ser um número racional, pois sabemos que os decimais para números racionais ou terminam ou se repetem. Temos aí um exemplo de número irracional.

Um número irracional é qualquer número que, posto em uma sequência numérica, não pode ser escrito como uma fração de números inteiros. Você, provavelmente, já ouviu falar do famoso número irracional ℼ = 3,14159…, que dá a razão entre a circunferência de um círculo e seu diâmetro. Embora seja uma razão, pelo menos um da circunferência ou diâmetro não é um número inteiro, portanto, ℼ não é um número racional. Outro número irracional é √2 = 1.41421…, que é o comprimento da diagonal de um quadrado cujos lados têm comprimento 1. 

Voltando ao nosso jogo, todos os números irracionais e racionais juntos preenchem nossa sequência numérica entre 0 e 1. Suponha que seu amigo Jorge pudesse pegar qualquer número entre 0 e 1 e escolhesse um número irracional para você adivinhar. Você provavelmente passaria um mau bocado tentando adivinhar o número certo! Assim como acontece no caso da expansão decimal repetida de 3/22, você não pode citar dígitos infinitos, de modo que esse jogo não parece muito justo. 

Vamos mudar o jogo para que você possa vencer! Jorge escolhe três coisas: um número para você adivinhar, uma série de números em que esse número se encontra e quão próximo deve ser o seu palpite. Com essas novas regras, Jorge escolhe o número ℼ e lhe diz: “Estou pensando em um número entre 2 e 10. Veja se consegue adivinhar com aproximação de 0,01 do meu número”. Nessa situação, o jogo é assim: 

Nessa nova versão de jogo, mesmo se Jorge mudar a aproximação, você sempre poderá chegar a essa distância de ℼ. Você só precisará acertar a parte do número inteiro e uma certa quantidade de casas decimais. Por exemplo, para ficar dentro de 0,1 de ℼ, você precisa acertar apenas a primeira casa decimal. Para ficar dentro de 0,01 de ℼ, você precisa acertar as duas primeiras casas decimais. E para ficar dentro de 0,001, precisa acertar as três primeiras casas decimais. Não importa quão perto seu palpite deva estar, você pode ganhar esse novo jogo adivinhando uma casa decimal de cada vez até ter casas decimais suficientes. 

Como já vimos, todo decimal que termina é um número racional. Se usarmos esse processo de nos aproximarmos cada vez mais de um número irracional, adivinhando cada vez mais casas decimais do número, poderemos obter um número racional que esteja o mais próximo possível do número irracional pretendido. Em nosso jogo, isso significa que não importa qual número irracional Jorge escolha, nem quão perto você tenha que chegar, você sempre encontrará um número racional que atenda aos requisitos. Nesse jogo, você pode sempre vencer! 

Conclusão

A razão pela qual isso acontece é que os números racionais são densos nos números reais. Isso significa que entre quaisquer dois números reais diferentes, sempre podemos encontrar um número racional. Como os números reais têm essa propriedade, podemos nos aproximar de qualquer número irracional com um número racional. Aproximar-se de um número irracional com um número racional é o que você faz no jogo em que Jorge escolhe um número irracional. 

Mas por que você precisaria aproximar um número irracional de um número racional? Suponha que esteja construindo uma estrutura de madeira para uma superfície triangular no formato de metade do quadrado da Figura 2. Você precisa cortar um pedaço de madeira com √2 pés de comprimento. Como você vai medir esse comprimento? Como √2 é um número irracional, você não poderá usar sua fita métrica para medi-lo com exatidão! Em vez disso, você escolherá um número racional que se aproxime da √2. Você pode escolher a quantidade de dígitos decimais para incluir em sua expansão e obter o pedaço de madeira mais próximo possível da √2, da mesma forma que escolheu seu número racional para estar tão próximo quanto Jorge queria que você chegasse no jogo. 

Figura 2. Dois números irracionais vistos na geometria.

A aproximação com números racionais é uma ferramenta muito poderosa para fazer cálculos, para medir materiais na construção e para muitas outras aplicações. O fato de os números racionais serem densos nos números reais é o que nos permite usar essa ferramenta! 

Glossário

Número racional: Número real que pode ser escrito como uma fração de dois inteiros a/b. As expansões decimais para os números racionais podem ser decimais finais ou repetitivos. 

Decimal final: Expansão decimal que possui apenas um número finito de dígitos decimais diferentes de zero. Por exemplo, 3,125 é um decimal final. 

Decimal repetitivo:  Expansão decimal onde os dígitos se repetem. Ou seja, por fim os dígitos formam um padrão que se repete para sempre. Por exemplo, 0,333… e 3,125353535… são decimais repetitivos. 

Número irracional: Número real que não pode ser escrito como uma fração de dois inteiros a/b. As expansões decimais para números irracionais são decimais infinitos que não se repetem. 

Conjunto denso de números: Um conjunto de números é denso em números reais se, para quaisquer dois números reais diferentes, houver um número do conjunto entre eles. Por exemplo, os inteiros não são densos nos números reais porque não há inteiro entre 2,1 e 2,2.  

Citação

Camenga, K. e Yates, R. (2020). “The real numbers: not all decimals are fractions.” Front. Young Minds. 8:4. DOI: 10.3389/frym.2020.00004. 

Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.