O que são as redes e qual a sua origem? 

A Torre de Babel é uma história bíblica na qual Deus confundiu a linguagem dos homens envolvidos na construção de uma torre que chegasse ao céu, e introduziu várias línguas no meio deles. Dessa forma, os homens não conseguiram mais se entender e tiveram de desistir da obra. De certa forma, as redes fornecem uma linguagem matemática que permite que cientistas de muitas áreas diferentes se entendam. Isso torna as redes ferramentas importantes para a solução dos problemas mais difíceis que se possa imaginar [1]. O campo de uso das redes para resolver problemas complexos é chamado de ciência de redes [2]. 

Os termos “gráfico” e “rede” são frequentemente usados de forma intercambiável. Tradicionalmente, um gráfico refere-se a um objeto matemático que não precisa ter uma representação do mundo real. Embora os matemáticos tenham estudado redes por mais de duzentos anos (pessoas como Euler e Cayley), a ideia de um gráfico é muito mais recente e pode ser rastreada até o matemático König na década de 1930,  <100 anos atrás. 

Na sua forma mais simples, um gráfico é matematicamente definido desta maneira: 

Definição 1.1: No par G = (V, E), onde V representa um conjunto finito de vértices e E o conjunto de arestas, E c (^V₂) é chamado de gráfico finito não direcionado. 

Essa definição pode ser entendida da seguinte forma: um gráfico é formado por apenas duas entidades, nós (também chamados de vértices e representados por V) e arestas (também chamadas de ligações e representadas pela letra E). Aqui, V é um conjunto que contém alguns elementos, p. ex., V={a, b, c, …} e E é outro conjunto que contém informação sobre as conexões entre os elementos em V, p. ex., E={(a, b), (a, c), …}. O termo (^V₂) denota outro conjunto que contém todos os pares possíveis de nós que podemos formar com os nós contidos no conjunto V. Portanto, o significado será semelhante aos coeficientes binomiais se V for um número inteiro positivo.

O símbolo c em E c (^V₂) significa que todos os elementos do conjunto E também estão contidos no conjunto (^V₂) e, portanto, E é um subconjunto de (^V₂). Esse é também o caso em que todos os elementos em (^V₂) estão também em E. Na Figura 1 (esquerda), temos um exemplo concreto de rede. 

O leitor pode estranhar a forma como a definição matemática da rede está escrita. Isso é o que se chama abstrato. Se alguém quiser se aprofundar no estudo das redes, saiba que tais formulações são inerentes ao campo e que entre suas habilidades deve estar incluída um grande interesse pela abstração em geral. 

Entre as primeiras redes matemáticas pesquisadas estão as redes aleatórias. Erdös e Rényi estudaram-nas em 1960. Um gráfico aleatório com N nós é obtido conectando-se cada par de vértices com uma probabilidade p fixada. Apesar da construção simples, o estudo das suas propriedades matemáticas é algo surpreendentemente complexo e gerações de cientistas trabalharam nesse problema. 

Onde encontramos redes? 

Na biologia, a importância das redes foi reconhecida porque os processos e sistemas biológicos precisam ser estudados holisticamente (ou seja, em relação a cada parte) [3]. Isso significa que os sistemas biológicos não podem ser reduzidos a partes arbitrariamente pequenas, pois o tamanho mínimo de uma parte ainda precisa ser funcional no sentido de que os organismos subjacentes funcionem. 

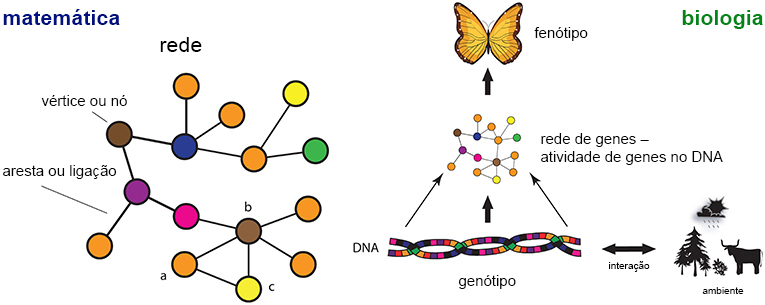
Uma das primeiras concepções a esse respeito foi a de Conrad Waddington, que apresentou a ideia de paisagem epigenética na década de 1940 [4]. Aqui, “epigenética” se refere ao estudo do fenótipo hereditário (veja a Figura 1), alterações que não modificam o DNA. Sua ideia básica é mostrada na Figura 1 (direita). No nível molecular dentro de uma célula biológica de um organismo (planta, animal ou humano), as interações entre genes e produtos gênicos (proteínas) podem ser representadas como uma rede gênica (por exemplo, uma rede reguladora de transcrição ou uma rede de proteínas).

Nessa rede, os nós correspondem aos genes e as arestas correspondem às interações entre os genes. Isso significa que as redes aparecem naturalmente no estudo das interações moleculares como sua visualização gráfica e representação matemática [5]. Dependendo do conteúdo do DNA de um organismo e de sua interação com o meio ambiente (dieta, estilo de vida, etc.), a estrutura da rede genética muda porque os padrões de atividade dos genes mudam também e, em consequência, o fenótipo (aparência física, como cor e forma das asas de uma borboleta) do organismo emerge. 

As redes podem ser usadas em muitos campos diferentes 

As redes são ferramentas bastante flexíveis e podem ser usadas em vários campos além da biologia. Essa flexibilidade é devida a três principais características das redes. Primeira: as redes podem tornar visíveis as complexas interações entre todas as partes diferentes de um sistema. Segunda: as redes formam uma representação matemática do sistema a ser estudado e manipulado. Terceira: a rede representa uma estrutura de dados que podem ser convenientemente armazenados em um computador e analisados de muitas maneiras diferentes, por exemplo, usando-se métodos estatísticos para encontrar comunidades de nós fortemente conectadas. 

Devido a essa flexibilidade, as redes são usadas em muitos campos diferentes, incluindo a química, a física, a biologia, a medicina, os negócios, as finanças e a mídia social. Aqui está uma lista das redes mais importantes desses campos e em quais estudos elas podem ser usadas. 

• Estruturas químicas, para estudar o modo como os compostos químicos estão relacionados uns com os outros. 
• Redes metabólicas, para estudar o modo como os organismos fazem tarefas como digestão da comida, crescimento e desenvolvimento. 
• Redes de sinalização, para estudar a comunicação molecular entre as proteínas. 
• Redes reguladoras transcricionais, para estudar a ativação dos genes. 
• Redes de interação de proteínas, para estudar formações complexas. 
• Redes financeiras, para estudar bons portfólios. 
• Estruturas de documentos baseadas em gráficos, para estudar estilos de escrita.
• Redes de comportamento do consumidor, para estudar hábitos de compras online. 
• Redes econômicas, para estudar os padrões de comércio global. 
• Redes sociais, para estudar relações humanas. 

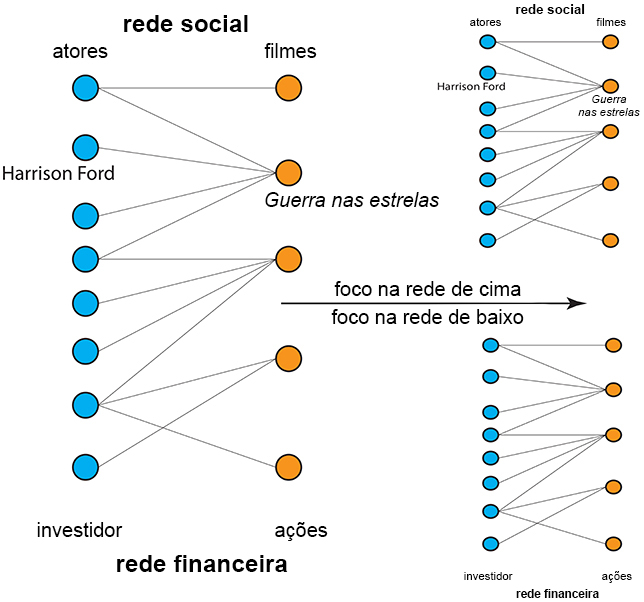
Na Figura 2, você pode ver dois exemplos de redes reais, de um tipo especial chamado rede bipartida. As redes bipartidas consistem de dois tipos de nós, mostrados por duas cores (azul e laranja). O significado desses nós depende do problema que está sendo estudado. Para as redes sociais mostradas, os nós azuis correspondem aos atores e os nós laranja aos filmes nos quais eles atuaram.

Por exemplo, o fato de Harrison Ford ter atuado em Guerra nas Estrelas é representado na Figura 2. Para a rede financeira mostrada, os nós azuis correspondem aos investidores e os nós laranja às ações compradas por eles. Mostramos a rede social e a rede financeira sobrepostas uma à outra porque queríamos enfatizar novamente o caráter abstrato das redes. Com relação a essas duas, você pode tornar a situação concreta concentrando-se em uma rede de cada vez e ignorando completamente a outra. Esse exercício o ensina a lidar com uma situação abstrata. 

O que significam as redes? 

O significado concreto e o uso das redes dependem dos problemas que elas representam. Por exemplo, podemos usar uma rede social para ver atores conectados aos mesmos filmes e descobrir quais apareceram juntos nos mesmos filmes. Na prática, isso poderia corresponder a um agrupamento de atores de acordo com o gênero do filme.

Para o modelo gráfico de uma proteína, estudam-se módulos ou estruturas de comunidades de vértices – na prática, eles podem corresponder a domínios evolutivamente conservados de proteínas. Para uma rede de computadores, estudaríamos quantos vértices podem ser removidos da rede sem que ela deixe de ficar conectada – na prática, isso muitas vezes indica a robustez de tal rede com relação a ataques de hackers. Para uma rede reguladora transcricional, podem-se identificar os nós com o maior número de conexões com outros nós – na prática, isso define genes centrais e pode revelar sua importância. 

Esses são apenas alguns exemplos que descrevem como as redes abstratas podem ser usadas para resolver problemas concretos em vários campos de pesquisa. 

Como obtemos as redes? 

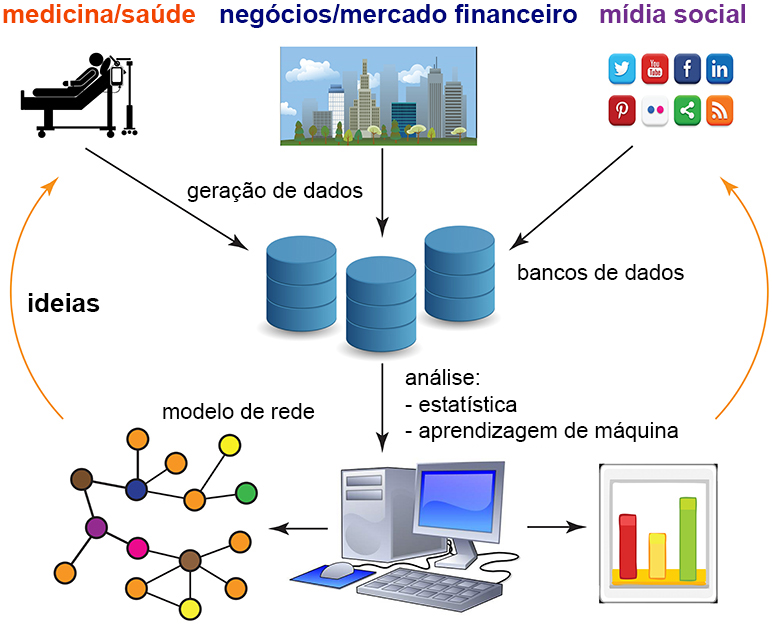
Em contraste com as redes mostradas na Figura 2, que são bastante simples e fáceis de entender, existem algumas mais abstratas. Elas precisam ser inferidas a partir de dados manipulados segundo métodos de estatística e aprendizagem de máquina. Na Figura 3, damos uma visão geral dos aspectos de nossa sociedade digital que nos permitem gerar grandes quantidades de dados sobre quase todos os aspectos da vida, incluindo saúde (exames médicos, smartphones, smartwatches, etc.), negócios (mercado de ações, Amazon, etc.) e redes sociais (Twitter, Facebook, etc.). Dados dessas áreas podem ser analisados com a ajuda de computadores para a produção de modelos de rede. Esses modelos de rede nos dão novas ideias sobre muitos aspectos da nossa sociedade, como economia, métodos de atendimento ao paciente ou comportamento do consumidor, que podem ser usados para nos ajudar a melhorar nossas vidas. 

Conclusão

Esperamos que nossa breve visão geral tenha mostrado que as redes fornecem uma linguagem básica para enfrentarmos os problemas mais interessantes e importantes da sociedade e da ciência. No entanto, para poder estudar esses modelos de rede, é necessário um profundo conhecimento de matemática. 

Glossário 

Definição matemática: Descrição expressa na linguagem da matemática, que é muito importante. 

Epigenética: Estudo das mudanças fenotípicas hereditárias que não envolvem alterações do DNA. Alude aos componentes que estão no topo (o prefixo grego epi significa “em cima”) dos genes. 

DNA: Ácido desoxirribonucleico, um material autorreplicante que está presente em quase todos os organismos vivos como o principal componente dos cromossomos e portador da informação genética. 

Referências

[1] Emmert-Streib, F., Dehmer, M. e Shi, Y. 2016. “Fifty years of graph matching, network alignment and network comparison.” Inform. Sci. 346–347: 180–97. DOI: 10.1016/j.ins.2016.01.074.

[2] Barabási, A.-L. 2013. “Network science.” Philos. Trans. R. Soc. A 371:20120375. DOI: 10.1098/rsta.2012.0375.

[3] Emmert-Streib, F. e Dehmer, M. 2011. “Networks for systems biology: conceptual connection of data and function.” IET Syst. Biol. 5:185. DOI: 10.1049/iet-syb.2010.0025.

[4] Waddington, C. H. 1957. The Strategy of the Genes. London: George Allen & Unwin.

[5] Emmert-Streib, F. e Glazko, G. V. 2011. “Network biology: a direct approach to study biological function.” Wiley Interdiscipl. Rev. Syst. Biol. Med. 3: 379–91. DOI: 10.1002/wsbm.134.

Citação

Emmert-Streib, F. e Dehmer, M. (2019). “Network science: from chemistry to digital society.” Front. Young Minds. 7:49. DOI: 10.3389/frym.2019.00049. 

Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.