Como os cientistas usam de estatística, amostras e probabilidade para responder a perguntas formuladas na pesquisa
Autores
Jovens revisores

Resumo
Estudos mostram que uma pessoa média faz cerca de vinte perguntas por dia! Algumas dessas perguntas são, é claro, bem simples, como indagar do professor se você pode ir ao banheiro; outras, porém, podem ser mais complexas, de difícil resposta. É aí que entra a estatística! Ela nos permite tirar conclusões de um conjunto de dados e por isso costuma ser chamada de “Ciência dos Dados”. Também ajuda profissionais da indústria a responder a perguntas de pesquisa ou negócios e prevê desfechos como o espetáculo a que você gostaria de assistir da próxima vez em seu aplicativo de vídeo favorito. No caso de um cientista social como o psicólogo, a estatística é uma ferramenta útil para fazer análise de dados e responder a perguntas de pesquisa.
Perguntas de pesquisa
Os cientistas fazem inúmeras perguntas que podem ser respondidas pela estatística. Por exemplo, um psicólogo pesquisador talvez esteja interessado no modo como o teste de desempenho é afetado pela quantidade de sono de um aluno na véspera. Psicólogos, biólogos e muitos outros tipos de cientistas procuram responder a perguntas sobre uma população ou um grupo de indivíduos. Digamos que um biólogo queira estudar um tipo específico de ave como população de pesquisa; que um psicólogo do desenvolvimento resolva pesquisar crianças de 3 a 6 anos; ou que um médico-cientista se interesse por pacientes com uma certa doença. O tipo de análise estatística a ser realizado dependerá da pergunta feita e das variáveis medidas. Variáveis são fatores, traços ou condições que podem existir em diferentes quantidades ou tipos, como altura, idade ou temperatura.
Amostras de uma população
Quando procuramos responder a perguntas de pesquisa, nem sempre é possível coletar informações de todos na população que nos interessa. Por exemplo, ao averiguar se o sono afeta o teste de desempenho, é praticamente impossível coletar informações sobre o sono e testar pontuações de cada estudante no mundo! Por isso, coletamos dados de uma amostra de indivíduos que melhor represente a população. É importante que as características da amostra sejam similares às da população como um todo. Os cientistas sociais se asseguram de que suas amostras tenham grupos etários e étnicos parecidos com os da população como um todo. Se não tivermos certeza de que nossas amostras apresentam o mesmo tipo de características da população em geral, haverá problemas para responder às nossas perguntas de pesquisa (Figura 1).
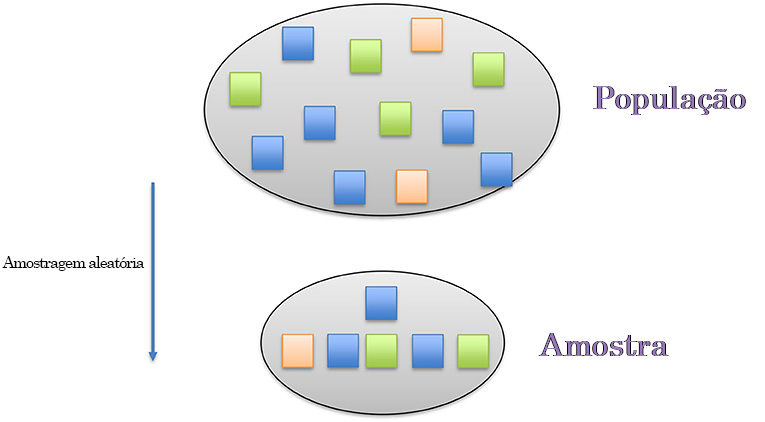
Figura 1. Amostragem aleatória é o método de escolha de uma amostra que represente acuradamente a população. Nesse método, cada indivíduo da população pode ser selecionado para a amostra. No exemplo, cada cor na população está presente também na amostra e as proporções de cada cor estão igualmente representadas nela.
Suponhamos que uma veterinária queira calcular o peso médio de todos os cães. Ela coleta uma amostra de cinco cães para pesar, encontra o peso médio da amostra e conclui que esse peso se situa entre 4,5 kg e 7 kg. Se você gosta de cães, talvez ache que há algo errado com esses números. Alguns cães são bem maiores e seria então de esperar que a média fosse mais alta. E se a veterinária coletou uma amostra apenas de chihuahuas? Nesse caso, não podemos dizer, é claro, que todos os cães pesam entre 4,5 kg e 7 kg: a amostra continha exemplares de apenas uma raça e não representava todos os tipos de cães. Se a veterinária tivesse uma amostra que representasse melhor a população de todos os cães, obteria sem dúvida uma média de peso bem diferente.
Um bom método de selecionar indivíduos para uma amostra que represente mais de perto uma população é a amostragem aleatória. Os cientistas a usam para garantir que cada indivíduo na população tenha igual probabilidade de ser selecionado – e isso assegura que a amostra seja mais parecida com a população em geral.
Estimativa com base numa amostra
Depois que o cientista reúne a amostra, talvez resolva tirar conclusões sobre ela e estender os achados à população inteira. Por exemplo, talvez queira saber o número médio de horas de sono de crianças de 12 anos à noite ou a altura média de alunos do curso colegial nos Estados Unidos. A fim de obter o valor de uma variável numa população (como a altura média), os cientistas recorrem à estimativa pontual a partir da amostra. Uma estimativa pontual é um número que calcula o verdadeiro valor de uma variável numa população (e muitas vezes ela é uma média).
Por exemplo, se quisermos encontrar o número médio de crianças por lar na cidade de Chicago, reuniremos uma amostra aleatória de famílias em Chicago e perguntaremos a cada uma delas quantas crianças vivem na casa. Em seguida, com base nessa informação, poderemos calcular o número médio de crianças nessas casas a fim de obter a estimativa pontual. Poderemos então concluir que o número médio de crianças em nossa amostra é bem parecido com o número médio de crianças em todas as casas de Chicago (Figura 2).

Métodos de medição e amostragem nunca são exatos, de modo que os cientistas aplicam intervalos de confiança à estimativa pontual a fim de obter um leque de valores que provavelmente contenha a verdadeira média de uma variável na população. Para calcular o intervalo de confiança, é necessário primeiro obter a margem de erro, ou seja, a quantidade calculada que aumentará ou diminuirá uma estimativa pontual. Trata-se de uma maneira de representar numericamente cálculos imprecisos ou erros na amostragem da população (por exemplo, quando uma amostra não é totalmente representativa da população).
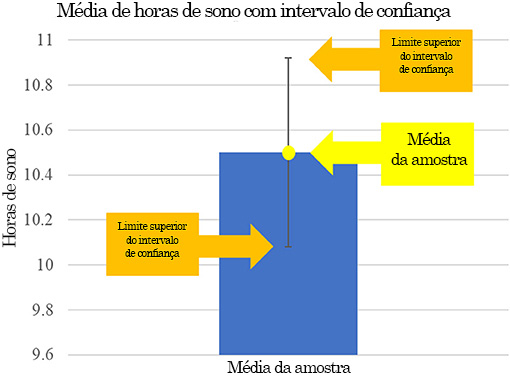
Vamos calcular um intervalo de confiança, para treinar! Imagine que coletamos uma amostra de 49 estudantes para um estudo do sono e descobrimos que a quantidade média de sono para eles é 10,5 h (nossa estimativa pontual). Em seguida, precisamos encontrar o desvio padrão, que é a distância entre o ponto de dados de cada pessoa e a média total. Um desvio padrão pequeno significa que quase todos os dados estão próximos, em valor, da média; e um grande desvio padrão significa que os dados estão mais espalhados por mais valores. Em nosso exemplo, digamos que o desvio padrão seja 1,5 h. Precisamos então calcular a margem de erro usando a seguinte fórmula:

Nessa fórmula, s representa o desvio padrão (1,5 h) e n se refere ao número de pontos de dados em nossa amostra (49 pessoas). Substituindo os símbolos por seus valores correspondentes, obtemos uma margem de erro de 0,42 h de sono. Para completar os intervalos de confiança, adicionamos a margem de erro à nossa estimativa pontual (ou a subtraímos dela) a fim de encontrar os limites superior e inferior do intervalo de confiança. Os psicólogos costumam usar o intervalo de confiança de 95% para calcular a margem de erro, ou seja, podemos ter certeza de que, em 95% do tempo, nosso intervalo de confiança encerra a verdadeira média da população. Nosso intervalo de confiança para a estimativa pontual, nesse exemplo, seria 10,5 +- 0,42 h ou 10,08 e 10.92. Isso significa que, em 95% do tempo, o número de horas de sono dos estudantes na população geral situa-se entre 10,08 e 10,92 h (Figura 3).
Os cientistas podem reduzir a margem de erro de várias maneiras a fim de tornar mais precisa sua estimativa da população. Uma delas é reunir mais indivíduos na amostra para que esta seja mais representativa da população. Outra maneira de reduzir a margem de erro é certificar-se de que a coleção de dados esteja o mais livre possível de erros a fim de minimizar a variabilidade desses dados, como, por exemplo, verificar se todas as ferramentas de medição (tabelas, levantamentos, réguas, etc.) são acuradas. Quanto mais acuradamente a amostra representar a população, graças ao emprego de amostragem aleatória e boas práticas de coleta de dados, menor será a margem de erro e mais preciso será o intervalo de confiança para a estimativa do verdadeiro valor da população.
Perguntas de pesquisa mais complexas
Às vezes, os cientistas querem ir além da descrição de cálculos simples como idade e altura médias nas populações a fim de compreender seus aspectos mais complicados. Digamos que não estamos interessados apenas em saber a quantidade de sono dos estudantes, mas em descobrir também quantos pontos haverá a menos no teste depois que eles perderem algumas horas de sono. Tamanhos de efeito são valores que estimam a magnitude de um fenômeno ou o grau em que uma variável (como as horas de sono) afeta outra variável (como o teste de pontuação).
Por exemplo, se dormir apenas 3 h abaixar seu teste em alguns pontos, em comparação com 9 h de sono, você não deve “perder o sono” por causa disso. Há uma diferença na pontuação, mas não muito grande. No entanto, se depois de perder 6 h de sono você cair muitos pontos no teste, isso terá um sério impacto em sua qualidade de vida. Então, você certamente concordará em que o efeito da perda de sono em sua saúde é importante.
Há várias maneiras de calcular o tamanho de efeito, dependendo da pergunta de pesquisa e do tipo de estatística usado pelo cientista. Depois de obter o tamanho de efeito, ele pode determinar se este é pequeno, médio ou grande. Os tamanhos de efeito permitem ao cientista, bem como a qualquer pessoa encarregada de revisar dados, entender melhor a influência que certas variáveis exercem em outras, na população.
Conclusões
Os cientistas fazem diversos tipos de perguntas e há muitas maneiras de responder a elas por meio da estatística. Os exemplos que discutimos neste artigo são maneiras pelas quais os cientistas respondem a questões simples com base em amostras. Mas a estatística não se limita a nenhum campo ou área específicos da pesquisa científica: ela tem ajudado cientistas a constatar a eficácia de determinados remédios e engenheiros a garantir a segurança do veículo que você dirige. E não para por aí: há incontáveis perguntas a que podemos responder por meio da estatística.
Glossário
População: Grupo identificado de indivíduos sobre os quais os cientistas fazem perguntas e querem obter respostas.
Variável: Fator, traço ou condição que existem em diferentes quantidades ou tipos medidos em pesquisa.
Amostragem aleatória: Maneira de selecionar indivíduos de uma população de modo a garantir que cada um deles tenha a mesma probabilidade de ser selecionado.
Estimativa pontual: Estimativa de determinado valor em uma população, como uma média.
Intervalos de confiança: Leque de valores atribuídos a estimativas pontuais que provavelmente contém o verdadeiro valor de uma variável na população.
Margem de erro: Quantidade calculada que se soma a uma estimativa pontual (ou dela se subtrai) para ser levada em conta em caso de imprecisão ou erro.
Desvio padrão: Distância média entre cada ponto de dados e a média total.
Tamanho de efeito: Valor que explicita a diferença entre médias de variáveis.
Leitura adicional
Cumming, G. 2013. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York, NY: Routledge.
Citação
Sandef, J. e Robbins, A. (2019). “How scientists use statistics, samples, and probability to answer research questions.” Front. Young Minds 7:118. DOI: 10.3389/frym.2019.00118.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br


