É fácil ou é difícil? Perguntas básicas na teoria da complexidade computacional
Autores
Jovens revisores

Resumo
Muitas coisas presentes em nossas vidas se destinam a resolver problemas. Seja um aplicativo em nossos celulares, a construção de um novo prédio ou o desenvolvimento de um novo medicamento, a resolução de problemas é um grande fator de motivação. Você sabia que existe um tipo fascinante de matemática por trás de muitos problemas complexos que enfrentamos em nossas vidas diárias? Essa matemática, chamada teoria da complexidade computacional, é um campo da ciência da computação. Trata-se de um campo ativo, em constante desenvolvimento, que está atraindo muitos jovens talentosos – como você! Neste artigo, descreveremos a teoria da complexidade computacional e os problemas para os quais ela foi projetada a fim de auxiliar a resolver. Esperamos que, ao terminar de lê-lo, você se convença de que a teoria da complexidade computacional é um dos campos mais interessantes da ciência.
Noa Segev é uma escritora de ciências e coordenadora de projeto na Frontiers for Young Minds. É bacharel em física e mestra em engenharia de energia renovável.
O professor Avi Wigderson ganhou o prêmio Abel, juntamente com László Lovász, por suas contribuições fundamentais para a teoria da computação e a matemática discreta, que tiveram um papel de destaque na elaboração de campos importantes da matemática moderna.
A teoria da complexidade computacional
Quando você ouve a palavra “computação”, provavelmente, pensa em números – talvez nos processos de adição e multiplicação que aprendeu nas aulas de aritmética de sua escola. Embora essas operações sejam de fato “cômputos” (cálculos), o termo “computação” é na verdade muito mais amplo e inclui vários desafios que enfrentamos na vida diária, como a necessidade de calcular como ir de um lugar a outro o mais rápido possível ou como manter informações sensíveis seguras graças ao uso da criptografia.
O campo da ciência da computação, que procura resolver diversos problemas complexos encontrados em nossas vidas diárias, é chamado de teoria da complexidade computacional. Cada problema de complexidade computacional tem uma entrada de dados e uma ou mais soluções válidas – nem sempre apenas uma.
Por exemplo: pense em um aplicativo de navegação, como o Google Maps. Esse aplicativo precisa resolver o problema de computação de como ir do ponto A ao ponto B da maneira mais rápida possível. Pode haver algumas rotas diferentes que levem você do ponto A ao ponto B no mesmo período de tempo: portanto, essa teoria da computação tem algumas soluções equivalentes. As entradas, nesse caso, são os pontos inicial e final (A e B) e as soluções (também chamadas de saídas) das computações são todas as rotas possíveis que você poderia seguir para ir do ponto A ao ponto B o mais rápido possível.
A solução de um problema computacional requer duas etapas (Figura 1). A primeira consiste em definir a função que conecta a entrada e a saída. Uma vez dada uma função, a segunda etapa pressupõe encontrar uma maneira eficiente de resolver o problema, de avaliar a solução ou de provar que o problema, por ser difícil, não pode ser resolvido em um tempo razoável – é essa a tarefa dos cientistas da computação que trabalham com a teoria da complexidade computacional.

Um importante problema da biologia – chamado enovelamento de proteínas – pode ser usado para demonstrar as etapas de resolução de um problema computacional. Como você deve saber, nossos corpos contêm máquinas biológicas minúsculas chamadas proteínas, que desempenham muitas das nossas funções vitais. As proteínas são formadas de cadeias de blocos de construção chamados aminoácidos (como um monte de miçangas em um cordão) e, depois de feitas, essas cadeias se enovelam em estruturas tridimensionais complexas. As proteínas só funcionam adequadamente quando se enovelam nas formas tridimensionais adequadas.
Os cientistas ainda não sabem quais são, exatamente, as leis físicas e químicas que fazem com que as proteínas se enovelem de uma maneira específica, quando poderiam se enovelar de milhões de outras formas. O enovelamento de proteínas é um problema computacional – para cada cadeia específica de aminoácidos (entrada), existe uma solução tridimensional específica que permite à proteína funcionar.
Cientistas têm criado vários modelos para tentar descrever como a sequência de aminoácidos de uma proteína determina sua estrutura tridimensional final. Um modelo utiliza a ideia de que a estrutura final da proteína é aquela que necessita de menos energia para preservar sua forma. Isso pode ser calculado somando-se as forças de atração ou repulsão de cada par de átomos que compõem a proteína [1]. Definir um modelo é a primeira etapa do processo de solução.
A próxima etapa é a computacional, que tenta determinar o grau de dificuldade no cálculo da solução do problema e descobrir a maneira mais eficiente de chegar à solução – que, nesse caso, é inferir a estrutura tridimensional final da proteína. Por exemplo, se a proteína tem apenas um pequeno número de átomos, é fácil calcular todas as forças que atuam entre cada par de átomos e somá-las para descobrir a estrutura tridimensional que requeira menos energia. Mas, se a proteína é composta por muitos átomos (isso acontece com a maioria das proteínas), torna-se muito mais difícil e, às vezes, até impossível calcular o enovelamento exato que resulta na energia mínima, mesmo se usarmos computadores muito poderosos.
Haverá, em casos assim, um cálculo melhor que permita encontrar a solução? Esse é o tipo de desafio que a teoria da complexidade computacional enfrenta.
A teoria da complexidade computacional aborda inúmeras questões práticas que estão relacionadas com nossas vidas cotidianas. Além de nos ajudar a construir modelos de sistemas que queremos compreender, como o do enovelamento de proteínas, a teoria da complexidade computacional também pode ser usada para determinar que tipos de problemas podem ou não ser resolvidos. Assim, saberemos até que ponto são eficientes os cálculos na resolução de problemas e desenvolveremos ferramentas práticas para essa tarefa. Parece complicado? Logo você verá que temos aqui um campo de pesquisa lindo e fascinante.
Algoritmos e eficiência
Um dos maiores problemas na teoria da complexidade computacional diz respeito à eficiência dos cálculos [2].
Cada cálculo é definido por uma série de operações que são realizadas na entrada para se chegar ao resultado. Essa série de operações se chama algoritmo. Todos nós usamos algoritmos em nossas vidas cotidianas. Por exemplo, aprendemos a somar números na escola. Você pode ter aprendido a somar de acordo com o algoritmo mostrado na Figura 2A. Quaisquer dois números podem ser somados, havendo, portanto, uma quantidade ilimitada de entradas no algoritmo de adição. As entradas podem ser um dígito, um milhão ou um bilhão de dígitos, por exemplo.
Os cálculos mais eficientes são como somar números: a quantidade de operações necessária no algoritmo é proporcional à quantidade dos números de entrada. Isso significa que, se tivermos de usar o algoritmo descrito na Figura 2A para somar números duas vezes maiores que os mostrados, precisaremos realizar o dobro de operações para obter o resultado final.
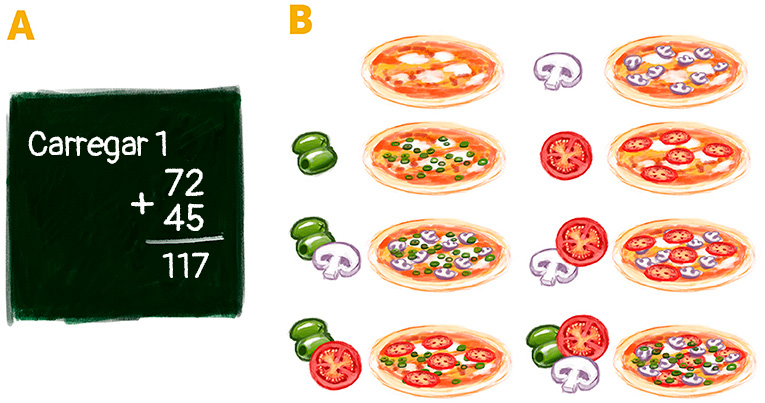
Agora, vejamos um problema um pouco mais difícil: a multiplicação de números. Na escola, provavelmente você também aprendeu um algoritmo para isso. Se usar o algoritmo mostrado neste vídeo para multiplicar números com o dobro da quantidade, a quantidade de operações que deverá realizar será 4 vezes maior. Por exemplo, se multiplicarmos números de dois algarismos, realizaremos quatro operações de multiplicação e mais algumas operações de soma. Porém, se os números tiverem dez algarismos, teremos de realizar 100 operações de multiplicação!
Mas, caso usemos o algoritmo mostrado para a soma, seriam necessárias apenas 10 operações para números de 10 algarismos. Se os números tiverem 100 dígitos, precisaremos realizar cerca de 10.000 operações para a multiplicação, em vez de cerca de 100 operações para a soma. Assim, no caso da multiplicação, a quantidade de operações é proporcional ao quadrado da quantidade de números.
A eficiência dos cálculos é muito importante porque define quais problemas podemos resolver dentro de um tempo razoável e quais não podemos, além do custo (em esforço e tempo) exigido para cada cálculo. Há muitos problemas que precisamos resolver rapidamente, para obter logo uma resposta (por exemplo, como o Waze, que tem de nos indicar instantaneamente a rota a seguir), e há outros que esperamos solucionar dentro de um tempo razoável (não necessariamente de imediato) para encontrar respostas a perguntas importantes (por exemplo, na ciência ou na engenharia).
Como você viu nos casos de soma e multiplicação, é grande a diferença entre a eficiência de um algoritmo proporcional à quantidade de entrada e a de um algoritmo proporcional ao quadrado da quantidade de entrada. Vejamos agora um caso em que o algoritmo é proporcional, não ao quadrado da quantidade de entrada, mas a um expoente ainda maior – digamos, de quinta ou sexta potência. Mas poderíamos pensar também no caso em que a eficiência do algoritmo é exponencial, ou seja, proporcional a 2 na potência da quantidade de entrada ou até mesmo um número maior na potência da quantidade de entrada. Esses casos exigem muitos cálculos para se chegar à solução.
Tais problemas complexos existem em nossas vidas cotidianas. Para demonstrar o significado de uma função exponencial, aqui está um exemplo saboroso: pense em sua pizza favorita. Digamos que a pizzaria ofereça uma cobertura possível: azeitonas verdes. Então, você pode escolher entre duas opções: uma pizza simples ou uma pizza com azeitonas verdes. Agora vamos supor que a pizzaria ofereça também uma cobertura de milho. Nesse caso, você pode escolher entre quatro opções: simples, com azeitonas verdes, com milho ou com azeitonas verdes e milho.
Se houvesse três coberturas (por exemplo, cogumelos, azeitonas e tomates), você teria oito possibilidades (Figura 3B). Portanto, nesse caso existem duas potências de opções de cobertura possíveis (23 = 8). Assim, o número de opções de combinações de coberturas de pizza é exponencial em relação ao número de coberturas, o que vem a ser basicamente a quantidade de entrada no cálculo. Para entradas maiores, como dezenas ou centenas de coberturas de pizza, o número de combinações de coberturas rapidamente se torna enorme.
Algoritmos exponenciais
O mesmo tipo de crescimento exponencial também se aplica a algoritmos exponenciais. Agora, ao invés de a quantidade de entrada crescer exponencialmente (como vimos com a quantidade de coberturas de pizza possíveis), é a quantidade de operações no algoritmo que pode crescer exponencialmente, sendo proporcional a algum número (digamos 2, como no exemplo da pizza) na potência da quantidade de entrada. Como a quantidade de operações que um computador pode realizar é finita – um bilhão de operações por segundo, talvez –, podemos traduzir a quantidade de operações no tempo necessário para o cálculo. Para um algoritmo exponencial e uma entrada de 20 caracteres, o tempo de cálculo desse computador será de apenas um milionésimo de segundo. Para uma entrada de 50 caracteres, o cálculo levará mais de 18 minutos – e, para uma entrada de 80 caracteres, mais de 3.800 anos!
Como há muitos cálculos que gostaríamos de poder realizar em um tempo razoável, uma questão importante na teoria da complexidade é o modo de encontrar os algoritmos mais eficientes para conseguir isso. Por exemplo, você pode ter aprendido uma maneira mais rápida que a descrita acima para multiplicar dois números (veja um exemplo aqui). Da mesma forma, seria possível encontrar formas mais eficientes de realizar outros cálculos para os quais temos apenas soluções ineficientes.
Os pesquisadores que estudam a teoria da complexidade computacional procuram esses algoritmos eficientes e, para fazer isso, devem também se perguntar como saberão que encontraram o algoritmo melhor e mais eficiente. Às vezes, eles conseguem provar que um algoritmo é o melhor possível para um problema específico; outras, tentam demonstrar que não existe uma maneira eficiente de resolver um problema específico para cada entrada, o que significa que o problema é inerentemente difícil.
Problemas de fácil e difícil solução
Agora, vamos dividir todos os problemas em dois grupos, dependendo de sua dificuldade (ou seja, de quanto tempo o computador levará para resolvê-lo) [2]. Chamaremos um grupo de P, de “polinômio”. Problemas de P podem ser resolvidos rapidamente porque a quantidade de cálculos necessários para resolvê-los é igual à quantidade de entrada elevada a uma potência. Por exemplo, ao somar números de acordo com nosso algoritmo, a quantidade de operações necessárias é um polinômio da primeira potência em relação à quantidade de entrada. Digamos que os problemas de P são todos aqueles que a humanidade pode resolver ou já resolveu.
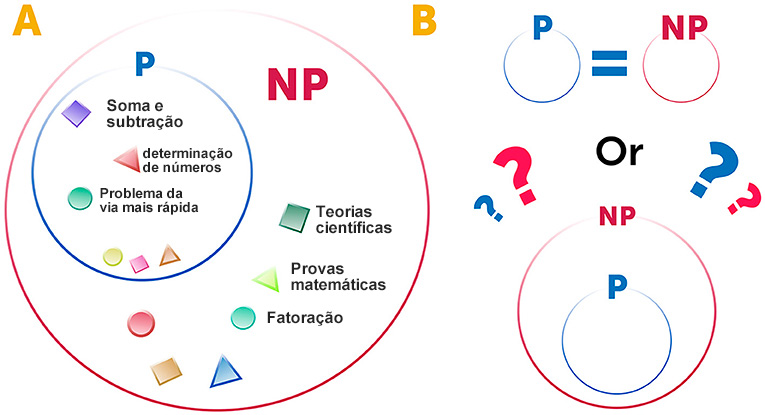
O segundo grupo de problemas é denominado PN, para “polinômio não determinístico”. Trata-se da série de problemas que ninguém resolveu ainda, mas que a humanidade gostaria de resolver. Os problemas de PN da vida real incluem, por exemplo, todos os problemas sobre os quais os cientistas se debruçam, todas as provas matemáticas que os matemáticos tentam validar e trabalhos de engenharia como o planejamento de uma ponte sobre um rio (Figura 3A).
Às vezes, um problema é difícil de resolver, mas, depois que se encontra uma solução, pode ser relativamente fácil verificar se ela está correta. Imagine um aplicativo de navegação estranho que precise encontrar a rota mais longa possível entre dois pontos, ao invés da mais curta. Esse é um problema difícil – encontrar a rota mais longa possível entre dois pontos é muito mais complexo que encontrar a mais curta. No entanto, se nos forem dadas todas as rotas possíveis entre dois pontos, será fácil verificar qual delas é a mais longa apenas comparando-as.
Em suma, mesmo se o cálculo do problema original for difícil, verificar uma solução sugerida será fácil. Como outro exemplo, se tentarmos encontrar todos os fatores de um número muito grande (ou seja, números que possam ser multiplicados para se chegar a esse número grande), teríamos aí um problema difícil. Ao contrário, se apenas precisarmos verificar se dois números são fatores de um número grande, esse seria um problema muito fácil – só precisaríamos multiplicá-los para verificar se a solução é igual ao número grande.
Uma das maiores questões em aberto na teoria da complexidade computacional é se as classes de problemas de PN e P são iguais ou se P é um subgrupo de PN (Figura 3B). Em outras palavras, caso possamos verificar facilmente se a solução de um problema está correta ou não, significará isso, em definitivo, que há um algoritmo capaz de resolver o problema com eficiência, mesmo ainda não tendo sido encontrado? Temos exemplos de problemas de PN para os quais ainda não encontramos soluções eficientes – mas isso não significa que tais algoritmos não existam, apenas que até agora não os encontramos. Caso existam e os encontremos, essa poderá ser a realização do maior sonho da humanidade.
Por outro lado, há alguns problemas que a nossa expectativa é que sejam difíceis de solucionar (isto é, não em P). Por exemplo, a segurança dos sistemas de criptografia de dados e outros sistemas de segurança eletrônicos, como os utilizados para compras online e baseados em cálculos extremamente complexos: quanto a esses, esperamos que sejam muito difíceis de resolver de forma eficiente. Se alguém encontrar um algoritmo capaz de resolver esses cálculos, todos os nossos sistemas de proteção de dados irão falhar e as informações atualmente criptografadas com rigor não estarão mais seguras. Fica claro então que há sérias implicações na questão de saber se P e PN são classes iguais de problemas.
Recomendações para mentes jovens
Nosso principal conselho é que você descubra aquilo de que gosta – qual é a sua paixão. As pessoas fazem o melhor possível e as coisas mais significativas quando acreditam na importância do que estão fazendo, e, muitas vezes, acham também divertido o que consideram importante. Você pode ter uma forte motivação para fazer algo de que, necessariamente, não gosta o tempo todo (por exemplo, talvez queira curar o câncer, mas não goste do trabalho em laboratório); porém, achamos que essa opção não é tão boa quanto encontrar algo que realmente aprecie.
Se você é bom em resolver problemas, recomendamos que aprenda o máximo possível e tente entender aqueles que gostaria de enfrentar. Depois de escolher uma área, procure ser o melhor que puder (Figura 4). A carreira acadêmica não é para todos, e algumas pessoas podem se divertir mais trabalhando em empresas especializadas na solução de problemas. Mas se você tem interesse na carreira acadêmica, desenvolva duas características importantes: uma sede insaciável de conhecimento e um amor por compartilhar esse conhecimento no ensino e na orientação de alunos. A paciência também é importante, juntamente com a capacidade de conviver de forma positiva em um ambiente competitivo.

Se você está especificamente interessado em pesquisa matemática, saiba que existem conexões entre subcampos que supostamente não se “comunicam” entre si. Dominá-las é indispensável, daí ser importante conhecer o maior número possível de áreas da matemática. Além disso, os matemáticos muitas vezes tentam resolver problemas que ninguém resolveu antes: portanto, se você seguir esse caminho, talvez não consiga também resolvê-los. Isso significa que poderá investir muito tempo em coisas que, em última análise, não darão certo.
Mas se você gosta do processo de resolução de problemas, mesmo que não tenha nenhuma garantia de êxito ou que seu progresso pareça extremamente lento, você ainda ficará feliz. Em outras palavras, bons pesquisadores de matemática devem adorar o processo de resolução de problemas, independentemente do que venham a conseguir. Por fim, vale lembrar que os pesquisadores estão sempre aprendendo com suas ideias, ainda que elas não levem ao sucesso na resolução do problema. O que aprendem durante o processo permanece com eles e pode ajudá-los a resolver problemas futuros.
Glossário
Algoritmo: Série de ações praticadas na entrada para se chegar ao resultado do cálculo com um número finito de passos.
Problemas de P: Problemas computacionais de fácil solução (polinomial em relação à quantidade de entradas). Problemas de PN: Problemas computacionais em que a verificação da solução é um problema de P. Esse algoritmo não fornece a solução, apenas certifica que uma solução sugerida está correta.
Referências
[1] Levinthal, C. 1968. “Are there pathways for protein folding?” J. Chim., Phys. 65:44–5. [2] Wigderson, A. 2019. Mathematics and Computation. Princeton, NJ: Princeton University Press.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br