Os cientistas podem prever quem são seus amigos?

Já foi dito: “O importante não é o que sabemos, mas quem conhecemos”. Você e seus amigos provavelmente têm muitas coisas em comum. Pode fazer uma lista delas? Quais são seus interesses e características em comum? Vocês estudam na mesma escola ou jogam no mesmo time? Moram no mesmo bairro ou cidade? Têm amigos em comum? Você provavelmente responderia sim a pelo menos algumas dessas perguntas para cada um de seus amigos mais íntimos. Pode não perceber, mas você e seus amigos também compartilham todo tipo de informação, atitudes e comportamentos acerca da escola.

Os cientistas descobriram que as pessoas ao seu redor, aquilo que elas sabem e pensam sobre a escola, e o modo como se comportam, podem influenciar seu futuro acadêmico [1]. Em outras palavras, seus amigos influenciam seus hábitos e seu desempenho na escola. Por outro lado, seu desempenho na escola pode influenciar a personalidade de seus amigos [2]! Acontece que os cientistas sociais e os matemáticos conseguem até prever, até certo ponto, quem são seus amigos! 

O que é uma rede social?

Os cientistas que estudam redes usam equações matemáticas para representar graficamente e medir comportamentos e qualidades de relacionamento, identificando as pessoas a quem você pede ajuda e a proximidade de amigos [3]. Uma redesocial é uma teia de conexões pessoais na qual os indivíduos trocam conhecimentos e recursos. A quantidade de conhecimento e recursos trocados em uma rede depende dos padrões e da qualidade dos relacionamentos dentro da rede [4].

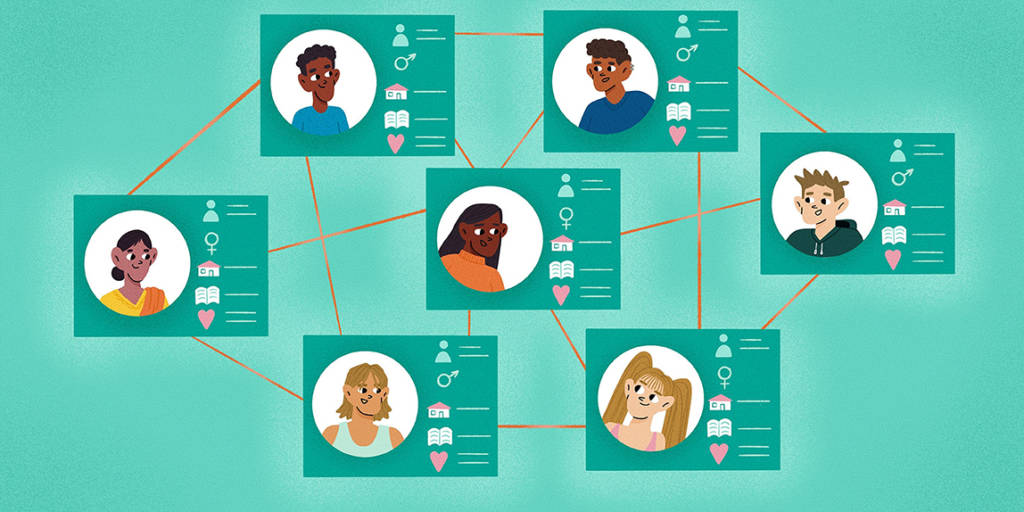
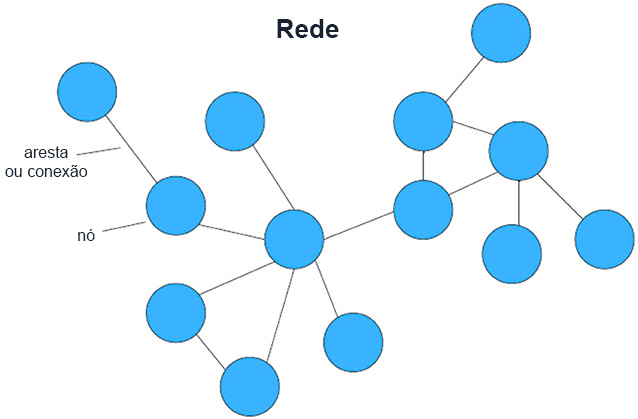
Podemos também visualizar as redes sociais criando gráficos. Nos gráficos das redes sociais, as pessoas são representadas por círculos coloridos chamados nós. As cores dos nós podem representar as características das pessoas na rede, como série na escola, idade ou sexo. As conexões entre as pessoas (por exemplo, amizades) são representadas por linhas entre nós, chamadas de arestas (Figura 1). 

Um modelo de grafos aleatório exponencial (MGAE) é uma ferramenta matemática avançada que prevê se duas pessoas podem se conectar com base nas características de uma rede. O MGAE compara todas as conexões aleatórias possíveis em uma rede para descobrir qual a probabilidade de duas pessoas se conectarem em algum momento no futuro. Então, basicamente, essa é uma ferramenta para prever conexões entre pessoas. 

Com nosso modelo simplificado, você pode fazer suas próprias previsões baseadas em apenas cinco perguntas. Tem alguém em mente? Ótimo! Vamos tentar! 

Qual a densidade de sua rede?

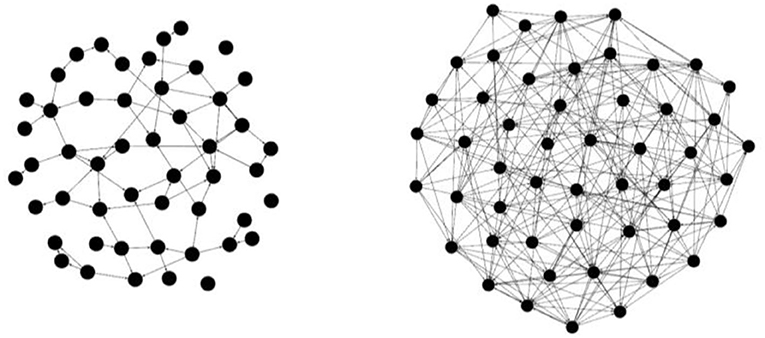
Você consegue imaginar um time ou clube atlético do qual faça parte e no qual quase todas as pessoas sejam amigas? Essa seria uma rede densa, onde realmente está a maioria das pessoas que poderiam ser amigas. A densidade é descrita com um valor percentual calculado como o número de conexões (ligações) reais em um grupo (rede) dividido por todas as conexões (ligações) possíveis no grupo (rede). Por exemplo, ambas as redes na imagem abaixo (Figura 2) têm 50 nós, mas a rede à direita tem muito mais conexões (linhas) entre nós, por isso é mais densa! 

A densidade é importante no cálculo do MGAE porque pode aumentar ou diminuir a probabilidade de duas pessoas se conectarem. Numa rede com um valor de densidade alto, a probabilidade de conexão entre dois indivíduos será muito maior. Ou seja, em uma rede muito densa, é muito mais provável que duas pessoas na rede acabem se conectando. 

Quantos amigos em comum você tem?

Você consegue pensar em alguns de seus amigos que também sejam amigos entre si? Isso étriangulação – quando as pessoas são amigas dos amigos dos seus amigos. É mais provável que você seja amigo dos amigos deles por causa disso. Em um gráfico de rede, essas conexões (linhas) fazem aparecer formas de triângulo, por isso ele é chamado de triangulação! Quando há muitos triângulos em um gráfico de rede, você obtém um valor de triangulação alto. Um valor de triangulação alto aumentaria a probabilidade de duas pessoas eventualmente se conectarem, enquanto um valor de triangulação baixo não a aumentaria tanto. 

Seus amigos o chamam de amigo?

Se lhe perguntássemos quem é o seu melhor amigo, você diria que essa pessoa também o considera o melhor amigo dela? Caso seja assim, está aí o que chamamos de reciprocidade. Outro exemplo: em uma rede de sala de aula, talvez um aluno liste você como a pessoa a quem ele procura quando precisa de ajuda e você também o lista como alguém a quem pede ajuda quando precisa. Em ambas as situações, as pessoas “enviam” conexões umas para as outras. Como a reciprocidade é uma forma de conectividade cada vez maior em uma rede, ela constitui um valor importante para o cálculo do MGAE. Tal como acontece com a densidade e a triangulação, um valor elevado de reciprocidade aumentaria a probabilidade de duas pessoas finalmente se conectarem. 

Você se aconselha com seus amigos?

Se lhe pedíssemos para elaborar uma lista de seus amigos e, em seguida, a das pessoas que procura para ajudá-lo a fazer o dever de casa e outra com as pessoas a quem recorre em busca de apoio nos momentos difíceis, você, provavelmente, teria pelo menos um amigo em mais de uma dessas listas. De acordo com os cientistas de rede, você teria muitos tipos de conexões (“arestas”) com esse amigo. Quando você tem vários tipos de conexões (“arestas”) com um indivíduo, isso é chamado de fenômeno de efeito de aresta. O termo efeito de aresta significa, basicamente, que se você passa muito tempo com um amigo, é provável que esteja conectado a ele de várias maneiras. Quanto mais efeitos de aresta houver em uma rede, maior será a probabilidade de duas pessoas por fim se conectarem, tornando esse valor igualmente importante para o cálculo de MGAE. 

Você compartilha características?

Você já ouviu a expressão “diga-me com quem andas e te direi quem és”? Já notou que muitas vezes compartilha com seus amigos gostos, desgostos, hobbies e talvez até crenças? Essa é a chamada homofilia quando as pessoas têm conexões com outras iguais a elas. Então, quando há mais homofilia em uma rede, as pessoas tendem a fazer mais conexões. Tal como as outras características da rede (densidade, triangulação, reciprocidade e efeitos de aresta), a homofilia pode aumentar ou diminuir a probabilidade de duas pessoas finalmente se conectarem, razão pela qual os cientistas de rede gostam de incluí-las nos cálculos de MGAE. 

A previsão dos amigos – como funciona?

As estimativas dos MGAEs são relatadas em unidades de “log-probabilidades” (o logaritmo de uma razão de probabilidades). Os matemáticos usam log-probabilidades porque é uma ferramenta fácil para combinar múltiplas variáveis de probabilidade. 

As probabilidades são as chances de sucesso (você ou eu ganhar o jogo) em comparação com as chances de fracasso (você ou eu perder o jogo). Por exemplo, digamos que há uma chance de 1 em 4 (0,25) de você ganhar (sucesso) e há uma chance de 3 em 4 (0,75) de você perder (fracasso). Para determinar suas chances de vitória, dividimos a chance de sucesso (0,25) pela chance de fracasso (0,75) e obtemos (0,25/0,75). 

Agora, digamos que eu não seja tão bom no jogo quanto você: então, a chance de eu ganhar é (0,10) e a chance de não ganhar é (0,9). Para obter minhas chances de ganhar, dividimos minha chance de sucesso (0,10) por minha chance de fracasso (0,9) e obtemos (0,10/0,9). 

Em seguida, para comparar as suas e as minhas chances de vencer, precisamos combinar as probabilidades criando uma razão, dividindo as suas probabilidades pelas minhas. A razão de probabilidades entre a nossa probabilidade de ganhar o jogo é escrita como (0,25/0,75)/(0,1/0,9), simplificada para 3. Em outras palavras, as probabilidades de você ganhar são 3 vezes maiores do que as minhas. 

Como vê, as razões de probabilidades são assimétricas. Em uma reta numérica típica, o número mais baixo é o infinito negativo, o número mais alto é o infinito positivo e o número “central” é zero. No entanto, para as razões de probabilidades, o número mais baixo possível é zero, o número mais alto é o positivo infinito e o número do “centro” é um! 

Pense assim: se eu tenho duas vezes mais chances de vencer você no tênis, você tem metade das chances de me vencer. Em termos de razão, elas são equivalentes, mas numericamente (2 e 0,5) estão a distâncias diferentes de 1 em uma reta numérica, e 1 significaria que temos chances iguais de vencer o outro. Então, recorremos ao logaritmo da razão de probabilidades. A função log tem muitos aspectos, mas o que é mais relevante para nós é que o log de 1 é 0 e para x positivo sabemos que log(x) = log(1/x). Por exemplo, o log de 2 é 0,69 e o log de 1/2 é -0,69. Então, se você calcular a razão de probabilidades como a chance de eu ganhar contra a chance de você ganhar, e vice-versa, com o log obtemos os mesmos números. Eles diferem apenas pelo sinal positivo/negativo. Em outras palavras, eles estão agora a distâncias iguais de 0 em uma reta numérica. 

Portanto, calcular o log das probabilidades altera as chances iguais para 0 e permite uma estimativa simétrica das probabilidades. Os matemáticos usam log-probabilidades porque é uma ferramenta mais fácil para combinar múltiplas razões de probabilidades, e isso é o que nossa calculadora interativa fará. Em nosso caso, podemos usar “pontos” no lugar de log-probabilidades. 

Uso da calculadora interativa

Nós escolhemos valores específicos para a calculadora interativa (modelo) abaixo com base em resultados típicos de redes sociais. Por exemplo, as chances de pessoas com amigos em comum serem amigas são altas (nesse caso, três vezes mais), mesmo em redes comumente menos densas, como as de amizade. 

Os números na calculadora interativa (modelo) abaixo (Figura 3) podem ser alterados dependendo de quais tipos de semelhança os modeladores consideram mais importantes para fazer amizade em determinada rede. Escolhas como “4 pontos para aconselhamento mútuo, 1 ponto para a mesma identidade de gênero” são apenas escolhas e não regras imutáveis. Uma grande parte da matemática aplicada consiste em ajustar um modelo para que ele represente a realidade com mais precisão. É verdade que, na pesquisa, certos tipos de semelhança parecem contribuir mais para a amizade em grandes redes escolares (por isso incluímos alguns deles abaixo). Por exemplo, se você tem amigos em comum, é muito provável que seja amigo deles e, se pede conselho a alguém na escola, é ainda mais provável que vocês sejam amigos. No entanto, esses valores são hipotéticos. 

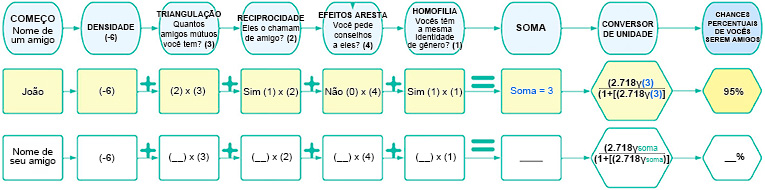
“Pontos” de amizade

Imagine duas pessoas indo para a mesma escola, você e eu! Grandes redes de amizade baseadas em escolas tendem a não ser muito densas, por isso começaremos com uma suposição de (baixa) densidade de rede que nos dá seis pontos negativos. Vamos imaginar que temos 2 amigos em comum (triangulação), o que acrescenta 6 pontos à pontuação. Você e eu dizemos que somos amigos (reciprocidade), a qual acrescenta mais 2 pontos à nossa pontuação. No entanto, nenhum de nós pede conselhos ao outro (efeitos de aresta), o que significa que não adicionamos esses pontos à nossa pontuação. Agora, digamos também que ambos compartilhamos a mesma identidade de gênero (homofilia), o que acrescenta mais 1 ponto à nossa pontuação. Somando nossa pontuação total, temos -6 + 6 + 2 + 0 + 1 = 3. 

Cálculo das probabilidades

Obtida a soma (3) de seus pontos de amizade, esta será a log-probabilidade de sermos amigos. Para converter isso em um número de amizade (percentagem de chance), precisamos calcular o log reverso. A fórmula da calculadora interativa faz exatamente isso! Ela converte suas log-probabilidades em chance percentual. Para fazer isso, elevamos o número de Euler (uma constante matemática que vale aproximadamente 2,718) ao expoente da soma de pontos de amizade, dividido por 1 mais o número de Euler elevado ao expoente da soma dos pontos de amizade. Quando inserimos os números de nosso exemplo na fórmula abaixo, obtemos 0,95, ou 95% de chance de sermos amigos. 

Sua vez!

Dependendo de suas respostas às perguntas abaixo, o valor final da pontuação MGAE mudará. Transformamos o valor da pontuação em uma percentagem quando você consegue tornar isso mais fácil em uma situação da vida real. Se o percentual for alto, acima de 50%, é provável que vocês sejam amigos. Se o percentual for baixo, abaixo de 50%, é provável que vocês não sejam amigos. 

Agora, você pode usar nossa calculadora MGAE interativa sozinho para descobrir as chances de ser amigo de uma pessoa real que conhece! 

Movimentos avançados

Se você quiser tentar algo um pouco mais avançado, experimente brincar com o modelo para alterar esses números e ver o que acontece – quais valores produzem as redes reais mais precisas? Afinal, é assim que funciona a modelagem da vida real.

 É importante lembrar que nosso exemplo de toda uma rede de amizade baseada na escola não é muito denso. Mas digamos que você queira tentar novamente com uma rede menor e mais densa, como um clube específico ou um programa extracurricular, como uma banda de rock ou um clube de palestras e debates. Seria difícil conhecer cada pessoa de sua escola, muito menos ser amigo de todas. Por outro lado, seria bem mais fácil conhecer todos em um pequeno grupo e fazer amizade com eles. No caso de um grupo ou clube pequeno, você provavelmente terá um coeficiente de densidade positivo na calculadora (como 3 ou 6 pontos, em vez de 6 negativo). Poderia até estimar a densidade real de uma pequena rede calculando as conexões de amizade reais existentes no grupo divididas pelo número total de conexões possíveis entre os indivíduos do grupo. 

Agora que você sabe como fazer isso, tente mapear sua própria rede social e usar seus próprios números de densidade na calculadora! Notará que, com o aumento da densidade, aumenta também a percentagem de chance de sermos amigos! Agora, você realmente está fazendo ciência de rede! 

Conclusão

Você talvez esteja pensando: por que alguém desejaria predizer quem serão meus amigos? Bem, acontece que há uma grande quantidade de aplicações para esse tipo de informação. A habilidade em predizer corretamente as conexões sociais é útil para encontrar “amigos” nos apps da mídia social e constitui uma oportunidade interessante para varejistas on-line, especialistas em marketing político ou aqueles que querem espalhar informações falsas, para só mencionar algumas situações.  Digamos apenas que, se o app é livre, então você e suas conexões sociais (redes sociais) são o produto. Phishing scams (fraudes eletrônicas) também manipulam suas redes sociais para espalhar vírus no computador, baixando todos os seus contatos e enviando-lhes um vírus como se você estivesse mandando um e-mail.

Epidemiologistas usam grandes modelos de predição de redes e rastreamento de contatos para tomar decisões sobre como melhor proteger você da propagação de doenças infecciosas. Mas amigos não trocam apenas germes e vírus de computador, eles trocam também ideias e atitudes sobre o mundo. Influenciam os comportamentos uns dos outros, incluindo exercícios, interesses, diversões e notas na escola. Não quer dizer que seus amigos precisem ser os maiorais da classe para você ser bem-sucedido na vida, mas, com base na matemática, certamente você não se prejudicará se ficar conectado com aqueles que vão bem na escola. Lembre-se, é também a qualidade de seus relacionamentos que importa. Agora você sabe: matematicamente falando, quem você conhece é um fator de muita importância! 

Glossário

Rede Social: Coleção de pessoas (nós) e as conexões (laços) entre elas (nós). 

Nós: Círculos que representam indivíduos em gráficos de redes sociais. 

Arestas: Linhas que conectam nós (pessoas) em gráficos de redes sociais.

MGAE: Ferramenta matemática avançada para prever conexões de pessoas em redes sociais. 

Densidade: Valor percentual de conectividade em uma rede social. 

Triangulação: Tendência das pessoas a serem amigas daquelas de quem seus amigos são amigos. 

Reciprocidade: Tendência das pessoas a “enviarem” conexões de volta para quem as enviou primeiro. 

Homofilia: Tendência das pessoas a serem amigas daquelas que são iguais a elas. 

Conflito de interesses

Os autores declaram que a pesquisa foi realizada sem nenhuma relação financeira ou comercial capaz de gerar um conflito de interesses. 

Referências

[1] Bourdieu, P. e Passeron, J. C. 1977. Reproduction in Education, Society and Culture. New York, NY: Oxford University Press.

[2] Ito, M. 2010. Hanging Out, Messing Around, and Geeking Out: Kids Living and Learning with New Media. Cambridge, MA: The MIT Press.

[3] Lin, N. 1999. “Building a network theory of social capital.” Connections 22:28–51.

[4] Daly, A. J., Moolenaar, N. M., Bolivar, J. M. e Burke, P. 2010. “Relationships in reform: the role of teacher’s social networks.” J. Educ. Administr. 48:359–91. DOI: 10.1108/09578231011041062. 

Citação

Black, A. e West, G. (2023). “Predict who your friends are?” Front. Young Minds. 11:820289. DOI: 10.3389/frym.2022.820289. 

Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.