O que é um caminho?

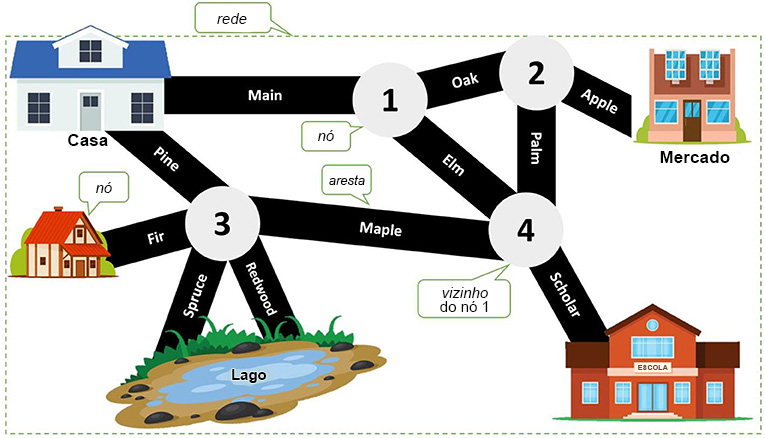
Diariamente, tomamos decisões sobre os trajetos a percorrer entre diferentes lugares. Em casa, podemos “viajar” entre o quarto e a cozinha; fora, entre a casa e a escola. Suponha que tenhamos uma rede de lugares conectados entre si por ruas e calçadas. Cada um desses locais é chamado nó, enquanto as ruas e calçadas recebem o nome de arestas. Os “vizinhos” de um nó são os nós aos quais ele está ligado por uma aresta. Um caminho é uma sequência de arestas entre um nó de origem e um nó de destino [1, 2].

Caminhos mais curtos

Em matemática, estudamos comprimentos de caminhos a fim de traçar caminhos mais curtos. E traçar caminhos mais curtos é, muitas vezes, bastante útil. Um caminho mais curto é aquele que, entre dois nós, possui menos arestas caso o custo da viagem ao longo de cada aresta seja o mesmo (por exemplo, quando cada aresta é uma rua do mesmo comprimento). De um modo mais geral, dados um nó de origem e um nó de destino, o caminho mais curto de um a outro é aquele que tem o menor custo total entre todos os caminhos da origem ao destino [1].

Para calcular o custo de um caminho, somam-se os custos individuais de todas as suas arestas. Um custo pode medir distância, tempo ou outra coisa. Por exemplo, no mapa da cidadezinha da Figura 1, um caminho mais curto da casa à escola pode ser aquele que consome a menor quantidade de tempo entre os caminhos possíveis. Pode haver mais de um caminho mais curto entre dois nós numa rede porque múltiplos caminhos às vezes têm o mesmo custo mínimo. Por isso dizemos “um” e não “o” caminho mais curto entre dois nós (embora isso realmente pareça estranho).

Você sem dúvida procura escolher caminhos mais curtos quando vai a diferentes lugares no dia a dia. Em nosso exemplo do “quarto à cozinha”, não faria muito sentido ir do quarto à lavanderia, da lavanderia ao quintal e finalmente do quintal à cozinha se quiséssemos apenas ir do quarto à cozinha. Seria bem mais rápido ir diretamente do quarto à cozinha sem passar primeiro pela lavanderia e pelo quintal.

Numa caminhada com localizações próximas umas das outras, existem poucas interseções de ruas (isto é, nós) e podemos testar a maioria dos diferentes caminhos para encontrar o mais curto. Entretanto, se os nós estiverem longe entre si – por exemplo, a casa, a escola e a loja de brinquedos em outra cidade –, então encontrar o caminho mais curto é bem mais difícil. De que modo as ferramentas de navegação, como o Google Maps, determinam o melhor caminho para se chegar a um destino? Uma das maneiras é resolver o problema do caminho mais curto, que é o problema matemático de encontrar um caminho entre dois nós de sorte a minimizar a soma dos custos de suas arestas¹.

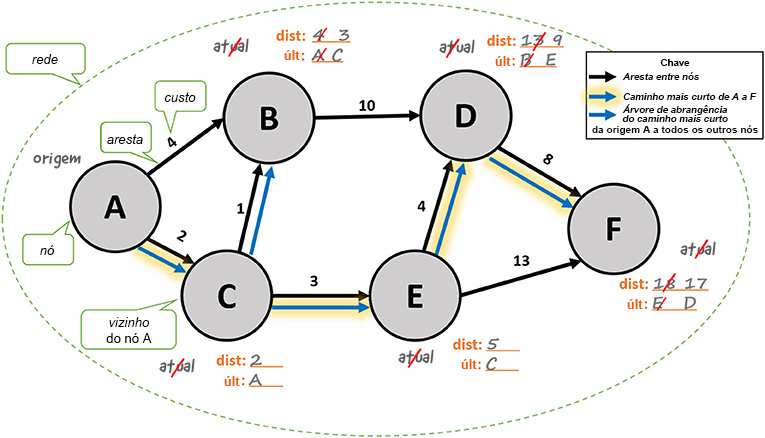
Em matemática, frequentemente identificamos nós usando números (ver as interseções na Figura 1) ou letras (ver a Figura 2). Para simplificar, também supomos que tudo seja bidimensional (como um desenho numa folha de papel): assim, mediremos a distância do modo como a mediríamos entre dois pontos no piso de nossa casa. Não consideraremos aspectos como altura ou curvatura da Terra. Na rede da Figura 2, se quisermos encontrar um caminho mais curto do nó A ao nó F, teremos de escolher as arestas de menor custo. Por exemplo, em vez de escolher a aresta com custo 4 do nó A ao nó B, escolheremos a aresta de custo 2 do nó A ao nó C. Escolher as arestas de menor custo a fim de encontrar o caminho mais curto é um dos elementos centrais do algoritmo de Dijkstra^{2, 3}.

Algoritmo de Dijkstra

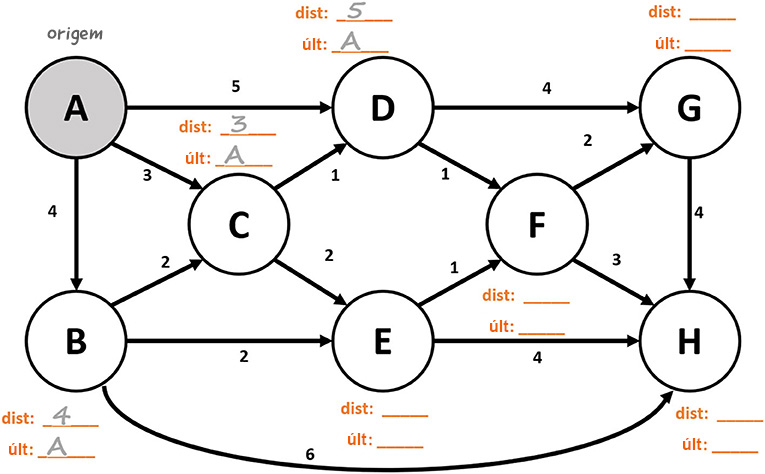
Um “algoritmo” é uma série precisa de passos a seguir para solucionar um problema [1]. O famoso algoritmo de Dijkstra, para resolver o problema do caminho mais curto, tem o nome de seu inventor, Edsger Dijkstra, um conhecido cientista da computação holandês⁴. Podemos usar esse algoritmo para criar uma árvore de abrangência do caminho mais curto (ver Figura 2) e encontrar o caminho mais curto de um nó de origem a todos os outros nós em uma rede, calculando separadamente a distância da origem a cada um dos outros nós. Nesta discussão, estamos usando a distância como custo, mas podemos usar o algoritmo de Dijkstra para qualquer outro tipo de custo. Na Figura 2, mostramos como usar esse algoritmo para construir uma árvore de abrangência do caminho mais curto em uma rede conectada. Acompanhe nossa explicação pela Figura 2.

Eis os passos a dar:

• Sombreamos o nó de “origem” (ver nó A na Figura 2). Para cada vizinho do nó de origem, estabelecemos o valor inicial de “dist” como a distância do nó de origem a esse vizinho e o valor inicial de “últ” como o nó de origem. No exemplo da figura 2, ao final desse passo, preenchemos os valores para “dist” e “últ” dos nós B e C. Para D, E e F, “dist” e “últ” continuam em branco.
• Identificamos o nó não sombreado com o valor “dist” mais baixo (excluindo as lacunas) e o consideramos nosso nó “atual”. Por exemplo, se começarmos pelo nó A como origem, então o nó atual será o C, pois a “dist” de A a C é menor que a “dist” de A a B. Havendo equivalência, escolheremos qualquer dos nós com o menor valor “dist”.
• Damos os seguintes passos para cada vizinho não sombreado de “atual”:
  A) Acrescentamos o “dist” de “atual” ao custo da aresta entre “atual” e o vizinho.
  B)Se o “dist” do passo 3a for menor que o “dist” do vizinho (ou se o “dist” do vizinho ainda estiver vazio), atualizaremos o “dist” do vizinho pelo “dist” que calculamos no passo 3a e poremos o “últ” do vizinho como nó atual.
• Depois de completar o passo 3 para todos os vizinhos não sombreados de “atual”, sombreamos “atual” e cruzamos o título “atual”.
• Se todos os nós estiverem sombreados, passamos ao passo 6. De outro modo, voltaríamos ao passo 2.
• Destacamos a aresta entre cada nó e seu nó “últ” para obter a árvore de abrangência do caminho mais curto a partir da origem.

Aplicações

Usando o algoritmo de Dijkstra, podemos encontrar um caminho mais curto de um nó de origem a qualquer outro nó em uma rede. Se você considerar sua casa o nó de origem e seu destino algum outro nó numa rede, poderá determinar uma boa rota de sua casa a qualquer lugar aonde quiser ir. Suponha que deseja visitar vários lugares antes de voltar para casa. Como encontrará o menor meio de visitar todos esses destinos minimizando despesas como gasolina, hotéis e tempo? Mais abstratamente, como encontrará o caminho mais curto que passe por todos os nós em uma rede, voltando depois ao nó de origem? Essa extensão do problema do caminho mais curto é conhecida como “problema da viagem do vendedor”⁶.

Encontrar caminhos mais curtos é importante para solucionar problemas em diferentes tipos de redes. Por exemplo, caminhos mais curtos podem aumentar a eficiência do planejamento urbano. Engenheiros civis podem representar uma cidade como uma rede e determinar as melhores localizações para abrir ruas com a finalidade de reduzir os congestionamentos de trânsito e instalar tubulações de água para uso da população [2]. Descobrir caminhos mais curtos também possibilita a transferência de dados de um computador a outro em alta velocidade, permitindo assim que grandes volumes de informação viajem em segundos [1, 2].

Há também inúmeros exemplos de caminhos curtos em comunicação e redes sociais. Suponha, por exemplo, que cada pessoa em uma rede social seja um nó e que cada aresta represente uma amizade. Você pode encontrar um meio de conectar uma pessoa de fora de seus grupos de amizade por meio das conexões de seus amigos. Os menores caminhos de conexão (como amizades) entre duas pessoas aleatoriamente escolhidas nos Estados Unidos são mais curtos do que se imagina. Em média, há menos de seis passos entre uma pessoa de origem e uma pessoa de destino nesse caminho [3]!

O típico encurtamento dos caminhos mais curtos entre pessoas ilustra o “fenômeno do mundo pequeno” e seus comprimentos inspiraram também a expressão “seis graus de separação” [1]. O segundo exemplo trata dos eventos correntes. Durante a pandemia da COVID-19, encontrar caminhos curtos tem sido útil para limitar a exposição ao vírus responsável pela doença. Por exemplo, no último ano e meio, para ir a um supermercado fazer compras era conveniente encontrar caminhos mais curtos (evitando contato com outras pessoas graças ao distanciamento físico) [4, 5].

Conclusão

Caminhos mais curtos são importantes para ir de um lugar a outro. Têm inúmeras aplicações em vários tipos de rede e podem resolver diversos problemas práticos. Do planejamento das férias da família ao exame de como nosso mundo está conectado, o estudo dos caminhos mais curtos em redes é incrivelmente importante e forma a base para pesquisas mais complexas.

Glossário

Rede: Conjunto de objetos (chamados “nós”) e suas conexões (chamadas “arestas”).

Nó: Objetos em uma rede conectados a outros objetos. Por exemplo, na Figura 1, cada localização e cada interseção de rua é um nó.

Aresta: Objeto que conecta dois nós. Por exemplo, quando você vai de casa à escola, cada rua é uma aresta.

Caminho: Sequência de arestas de um nó de origem a um nó de destino.

Custo: Medida da quantidade de esforço exigido para percorrer uma aresta numa rede. Na vida real, um custo pode medir distância, tempo ou algo mais.

Caminho mais curto: Caminho de um nó de origem a um nó de destino que apresenta o menor custo total entre todos os caminhos que fazem essa ligação.

Árvore de abrangência do caminho mais curto: Parte de uma rede de conexão que começa em um dado nó de origem e determina o caminho mais curto entre ele e cada um dos outros nós na rede. Por exemplo, se uma rede tem seis nós, existem cinco desses caminhos mais curtos na árvore de abrangência do caminho mais curto. Uma árvore de abrangência em uma rede inclui todos os nós dessa rede. Além do mais, como uma árvore de abrangência é um tipo de rede conhecido como “árvore”, qualquer um de seus pares de nós terá exatamente um caminho entre eles.

Agradecimentos

Agradecemos aos nossos jovens leitores – Nia Chiou, Taryn Chiou, Zoë Chiou, Tycho Elling e Sage Hansen – por seus muitos comentários úteis. Agradecemos também a seus familiares – Lyndie Chiou, Christina Chow, Tim Elling e Sterling Hansen – por nos colocar em contato com eles e permitir assim que solicitássemos sua colaboração. Somos gratos igualmente a Lyndie Chiou, Michelle Lee, Thomas Rexin e Akrati Saxena por suas valiosas observações. Gratos também a nossos jovens revisores e seus mentores pelas inúmeras e excelentes sugestões. MAP agradece o apoio da National Science Foundation (Grant Number 1922952) por meio do programa Algorithms for Threat Detection (ATD).

Referências

[1] Newman, M. E. J. 2018. Networks, 2ª ed., Oxford, UK: Oxford University Press.

[2] Cramer, C., Porter, M. A., Sayama, H., Sheetz, L. e Uzzo, S. (orgs.). 2015. Network Literacy: Essential Concepts and Core Ideas, disponível online em http://tinyurl.com/networkliteracy.

[3] Milgram, S. 1967. “The small-world problem.” Psychol. Today 1:61–7. DOI: 10.1037/e400002009-005.

[4] Brooks, H. Z., Kanjanasaratool, U., Kureh, Y. H. e Porter, M. A. 2021. “Disease detectives: using mathematics to forecast the spread of infectious diseases.” Front. Young Minds 9:577741. DOI: 10.3389/frym.2020.577741.

[5] Ying, F. e O’Clery, N. 2021. “Modelling COVID-19 transmission in supermarkets using an agent-based model.” PLoS ONE 16:e0249821. DOI: 10.1371/journal.pone.0249821.

Apêndice

Respostas

Atividade 1: Um caminho possível é Main, Elm, Scholar. Outro é Main, Oak, Palm, Scholar. Um terceiro é Pine, Maple, Scholar.

Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.