Números primos: por que são tão empolgantes?
Autores
Jovens revisores
Israel Arts and Science Academy
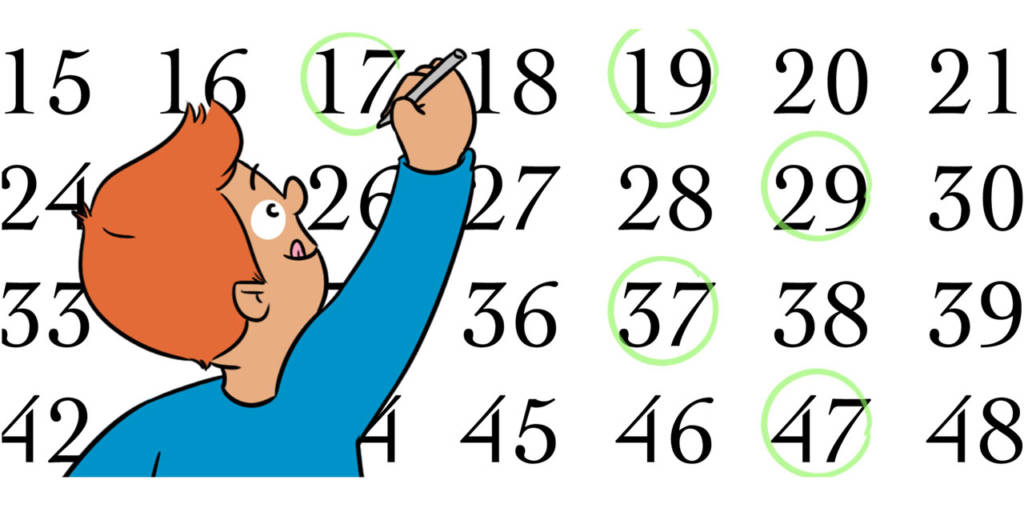
Resumo
Os números primos chamam a atenção dos homens desde os primórdios da civilização. Vamos explicar o que são, por que seu estudo entusiasma tanto matemáticos quanto leigos e, ao mesmo tempo, abriremos uma janela para o mundo da matemática.
Desde o começo da história humana, os números primos despertaram a curiosidade dos homens. O que são esses números? Por que é tão difícil responder às perguntas que se fazem sobre eles? Uma das coisas mais interessantes sobre os números primos é sua distribuição entre os números naturais. Em pequena escala, o surgimento de números primos parece aleatório, mas, em grande escala, pode haver um padrão que ainda não foi plenamente entendido. Neste pequeno texto, tentaremos acompanhar a história dos números primos desde os tempos antigos e aproveitar a oportunidade para mergulhar no mundo da matemática e entendê-lo melhor.
Números compostos e números primos
Você já se perguntou por que o dia é dividido exatamente em 24 h e o círculo em 360 graus? O número 24 tem uma propriedade interessante: pode ser dividido em partes iguais inteiras de vários modos. Por exemplo, 24 ÷ 2 = 12; 24 ÷ 3 = 8; 24 ÷ 4 = 6, etc. (complete você mesmo o resto das opções!). Isso significa que o dia pode ser dividido em partes iguais de 12 h cada uma, dia e noite. Numa fábrica que trabalhe em turnos ininterruptos de 8 h, cada dia é dividido exatamente em três turnos.
Também por isso é que o círculo foi dividido em 360º. Se ele for dividido em duas, três, quatro, dez, doze ou trinta partes iguais, cada parte conterá um número de graus inteiro. (Há outras maneiras de dividir o círculo que não mencionaremos.) Nos tempos antigos, dividir o círculo em setores de igual tamanho com grande precisão era necessário por vários motivos: artísticos, astronômicos e de engenharia. Os únicos instrumentos disponíveis eram o compasso e o transferidor, de modo que a divisão do círculo em setores iguais tinha enorme valor prático.1
Um número inteiro que possa ser escrito como produto de dois números menores é chamado de número composto. Por exemplo, as equações 24 = 4 x 6 e 33 = 3 x 11 mostram que 24 e 33 são números compostos. Um número que não possa ser decomposto dessa maneira é chamado de número primo. Os números 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29 são todos primos – na verdade, os primeiros dez números primos (se você quiser, faça as contas!).
Essa curta lista de números primos revela alguns dados interessantes. Primeiro, com exceção do número 2, todos os números primos são ímpares, pois um número par é divisível por 2, o que o torna composto. Assim, a distância entre dois números primos numa sequência (chamados números primos sucessivos) é de pelo menos 2. Em nossa lista, encontramos números primos sucessivos cuja diferença é exatamente 2 (como nas duplas 3, 5 e 17, 19). Há também espaços maiores entre números primos sucessivos, como o de seis números entre 23 e 29; cada um dos números 24, 25, 26, 27 e 28 é composto.
Outra observação interessante é que, tanto no primeiro quanto no segundo grupo de dez números (ou seja, entre 1–10 e 11–20), há quatro números primos, mas no terceiro grupo de dez (21–30) há somente dois. O que significa isso? Os números primos vão ficando mais raros à medida que a sequência avança? Pode alguém nos garantir que conseguiremos encontrar mais e mais números primos indefinidamente?
Se, a esta altura, você já está entusiasmado e quer continuar investigando a lista dos números primos e as questões que levantamos, isso quer dizer que tem alma de matemático. Pare! Não continue lendo!2 Pegue lápis e papel. Escreva todos os números até 100 e marque os primos. Descubra quantas duplas com uma diferença de 2 estão ali. Descubra também quantos números primos existem em cada grupo de 10. Percebeu algum padrão? Ou a lista de números primos até 100 lhe parece aleatória?
Um pouco de história e o conceito de teorema
Os números primos chamam a atenção dos homens desde os tempos antigos e já foram até associados com o sobrenatural. Mesmo hoje, algumas pessoas tentam atribuir propriedades místicas a esses números. O conhecido astrônomo e divulgador de ciência Carl Sagan escreveu, em 1985, um livro intitulado Contact [Contato], que falava de extraterrestres (uma cultura fora da Terra semelhante à humana) tentando se comunicar conosco por meio de sinais de números primos. A ideia de que sinais inspirados em números primos possa servir de base para nos comunicarmos com culturas extraterrestres continua a atiçar a imaginação de muitas pessoas até hoje.
Presume-se, comumente, que um interesse sério pelos números primos tenha começado nos tempos de Pitágoras. Pitágoras foi um antigo matemático grego. Seus discípulos, os pitagóricos – em parte cientistas, em parte místicos – viveram no século VI a. C. Não deixaram nada escrito e o que sabemos deles vem de histórias transmitidas oralmente de geração em geração.
Trezentos anos depois, no século III a. C., Alexandria (no atual Egito) era a capital cultural do mundo grego. Euclides (Figura 1), contemporâneo em Alexandria de Ptolomeu I, talvez você conheça por causa da geometria euclidiana, denominada em alusão a ele. A geometria euclidiana vem sendo ensinada nas escolas por mais de dois mil anos. Mas Euclides também se interessava por números. No livro IX de sua obra, Elementos, aparece na Proposição 20, pela primeira vez, uma prova matemática do teorema segundo o qual os números primos são infinitos.

Aqui é um bom lugar para dizer algumas palavras sobre os conceitos de teorema e prova matemática. Um teorema é uma asserção expressa em linguagem matemática da qual se pode afirmar, com certeza, que é válida ou inválida. Por exemplo, o teorema “os números primos são infinitos” assevera que no sistema de números naturais (1, 2, 3…) a lista de números primos não tem fim. Para sermos mais exatos, esse teorema assevera que, se escrevermos uma lista finita de números primos, sempre conseguiremos encontrar outro número primo que não está nela.
Para provar esse teorema, não basta acrescentar mais um número primo numa dada lista. Por exemplo, se incluirmos 31 como um número primo fora da lista dos primeiros 10 primos mencionados antes, mostraremos na verdade que essa lista não incluía todos os números primos. Porém, tendo acrescentado 31, encontramos todos os números primos e não há mais nenhum outro? O que precisamos fazer, e Euclides fez isso há 2.300 anos, é provar convincentemente que, para qualquer lista finita, por mais longa que seja, podemos encontrar um número primo não incluído nela. Na próxima seção, mostraremos a prova de Euclides, mas sem aborrecer você com um excesso de detalhes.
A prova de Euclides para a existência de números primos infinitos
A fim de provar que os números primos são infinitos, Euclides recorreu a outro teorema básico que ele conhecia, segundo o qual “todo número natural pode ser escrito como produto de números primos”. É fácil nos convencermos da verdade dessa última afirmação. Se você pegar um número que não seja composto, esse número será primo. De outro modo, você poderia escrever o número escolhido como produto de dois números menores. Se cada um dos números menores for primo, você terá escrito seu número como produto de números primos. Se não, escreverá os números compostos menores como produtos de números menores ainda, e assim por diante.
Nesse processo, você continuará substituindo qualquer dos números compostos por produtos de números menores. Como é impossível fazer isso para sempre, o processo tem que terminar e todos os números menores que você obteve não poderão mais ser decompostos: portanto, são números primos. Como exemplo, vamos decompor o número 72 em seus fatores primos:
72 = 12 x 6 = 3 x 4 x 6 = 3 x 2 x 2 x 6 = 3 x 2 x 2 x 2 x 3
Partindo desse fato básico, podemos agora explicar a elegante prova de Euclides para a infinitude do conjunto de números primos. Demonstraremos a ideia usando a lista dos primeiros 10 primos, mas você deve observar que essa mesma ideia funciona para qualquer lista de números primos. Multipliquemos todos os números da lista e acrescentemos 1 ao resultado. Vamos chamar de N o número obtido. (O valor de N na verdade não importa, pois o argumento é válido para qualquer lista.)
N = (2 x 3 x 5 x7 x 11 x 13 x 17 x 19 x 23 x 29) + 1
O número N, como qualquer outro número natural, pode ser escrito como produto de números primos. Quais são esses primos, os fatores primos de N? Não sabemos porque não os calculamos, mas de uma coisa temos certeza: todos dividem N. Todavia, N deixa um resto de 1 quando dividido por qualquer dos números primos de nossa lista, 2 3, 5, 7, …, 23, 29. Supõe-se que essa seja uma lista completa de nossos primos, mas nenhum deles divide N. Portanto, os fatores primos de N não estão na lista e, sobretudo, deve haver novos primos além de 29.
O crivo de Eratóstenes
Você encontrou todos os números primos menores que 100? Examinou cada número individualmente para ver se ele é divisível por números menores? Se fez isso, então gastou muito tempo. Eratóstenes (Figura 1), um dos maiores estudiosos do período helenístico, viveu poucas décadas depois de Euclides. Foi o diretor da biblioteca de Alexandria, a primeira biblioteca da história e a maior da antiguidade. Interessava-se não apenas por matemática, mas também por astronomia, música e geografia, tendo sido o primeiro a calcular a circunferência da Terra com uma precisão incrível para a época. Entre outras coisas, ele descobriu uma maneira inteligente de encontrar todos os números primos até um dado limite. Como esse método se baseia na ideia de passar pelo crivo (peneirar) os números compostos, chama-se crivo de Eratóstenes.
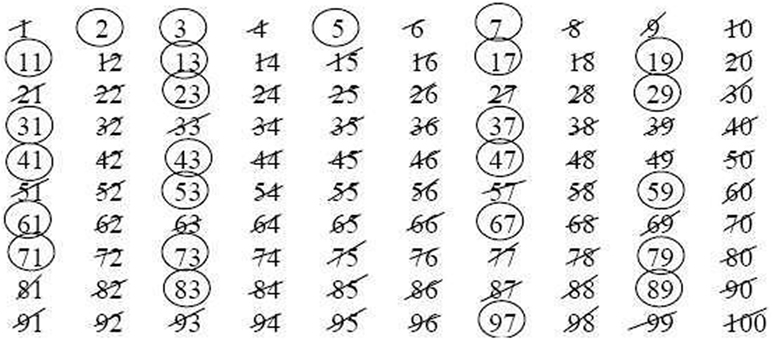
Vamos utilizar o crivo de Eratóstenes numa lista de números primos menores que 100, apresentada na Figura 2. Circule o número 2, que é o primeiro primo, e em seguida risque todos os seus múltiplos maiores, ou seja, todos os números compostos pares. Passe para o próximo número não riscado, o 3. Como ele não foi riscado, não é produto de números menores e podemos circulá-lo sabendo que é primo. De novo, risque todos os seus múltiplos maiores. Observe que alguns deles, como o 6, já foi riscado, enquanto outros, como o 9, serão riscados agora. O próximo número não riscado (5) será circulado. Novamente, risque seus múltiplos maiores: 10, 15 e 20 já o foram, mas 25 e 35, por exemplo, devem sê-lo agora. Continue da mesma maneira.
Até quando? Tente descobrir por que, depois de 10 = √100, não precisamos ir adiante no processo. Todos os números menores que 100 que não foram riscados são primos e podem ser circulados com segurança!
Frequência dos números primos
Qual é a frequência dos números primos? Quantos números primos existem, aproximadamente, entre 1.000.000 e 1.001.000 (um milhão e um milhão e um mil) e entre 1.000.000.000 e 1.000.001.000 (um bilhão e um bilhão e um mil)? Podemos estimar o número de primos entre um trilhão (1.000.000.000.000) e um trilhão e um mil (1.000.000.001.000)?
Os cálculos mostram que os números primos vão se tornando mais e mais raros à medida que a numeração aumenta. Mas será possível formular um teorema acurado que expresse exatamente quão raros se tornam? Esse teorema foi apresentado primeiro como uma conjectura pelo grande matemático Carl Friedrich Gauss em 1793, quando ele tinha 16 anos.
O matemático Bernhard Riemann, no século XIX (Figura 1), que influenciou o estudo dos números primos nos tempos modernos mais que qualquer outro, desenvolveu novas ferramentas para tratar o problema. Mas uma prova formal do teorema só foi dada em 1896, um século depois de sua formulação. Fato curioso, duas provas independentes foram apresentadas no mesmo ano pelo francês Jacques Hadamard e o belga De La Vallée-Poussin (Figura 1). Vale notar que os dois nasceram mais ou menos na época da morte de Riemann. O teorema que apresentaram recebeu o nome de “teorema dos números primos” devido à sua importância.
A formulação precisa do teorema dos números primos, e mais ainda os detalhes de sua prova, exigem uma matemática avançada que não podemos discutir aqui. Mas, simplificando, o teorema dos números primos estabelece que “a frequência dos números primos em torno de x é inversamente proporcional à quantidade de algarismos em x”.
No exemplo acima, a quantidade de primos em uma “janela” com a extensão de 1.000 em torno de um milhão (isto é, o intervalo entre um milhão e um milhão e um mil) será 50% maior que a quantidade de primos na mesma “janela” em torno de um bilhão (a razão é 9:6, tal como a razão entre a quantidade de zeros em um bilhão e um milhão) e cerca de duas vezes a quantidade de primos na mesma “janela” em torno de um trilhão (onde a razão da quantidade de zeros é 12:6). De fato, cálculos por computador mostram que há 75 números primos na primeira “janela”, 49 na segunda e apenas 37 na primeira, entre um trilhão e um trilhão e um mil.
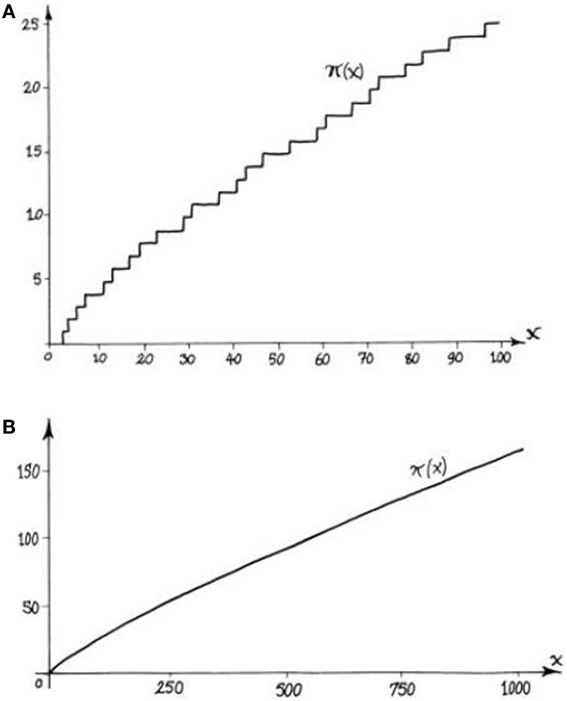
Essa mesma informação pode ser mostrada sob a forma de gráfico (Figura 3). Você notará que a quantidade Π(x) de primos até x muda na série x ≤ 1.000 e de novo em x ≤ 1.000. Observe que, quando encontramos um novo primo ao longo do eixo x, o gráfico sobe 1, tomando a forma de degraus (Figura 3A). Em pequena escala, é difícil detectar um padrão no gráfico. Muito fácil é provar que podemos descobrir arbitrariamente intervalos grandes, onde não há números primos, ou seja, espaços onde o gráfico não sobe. Por outro lado, uma célebre conjectura (ver abaixo) declara que existem infinitos números primos gêmeos, isto é, duplas de primos com a diferença de 2 entre si, o que equivaleria a um “degrau” com a largura de 2 no gráfico. Em grande escala, porém, o gráfico apresenta uma curva suave (Figura 3B), que demonstra o teorema dos números primos.
O fato de um fenômeno matemático parecer se comportar aleatoriamente em uma escala, mas mostrar regularidade (curva suave) em uma escala diferente/maior – regularidade que se torna mais e mais acurada à medida que a escala aumenta –, não é novo em matemática. Sistemas de probabilidade, como o jogo de cara-ou-coroa, se comportam da mesma maneira. É impossível prever o resultado de um único lance, mas, com o tempo, caso a moeda não seja adulterada, ela mostrará “cara” metade das vezes. Fato surpreendente é que o sistema de números primos não é probabilístico, mas ainda assim se comporta de muitas maneiras como se fosse aleatório.
Sumário: quem quer ser milionário?
A teoria dos números, que inclui o estudo dos primos, encerra incontáveis problemas não resolvidos, abordados sem sucesso pelas mentes mais brilhantes durante séculos. Alguns desses problemas em aberto são asserções matemáticas que ainda não foram provadas, mas em cuja correção não podemos deixar de acreditar. Problemas não resolvidos são chamados de “conjecturas” ou “hipóteses”. Já mencionamos a conjectura sobre a existência de números primos gêmeos infinitos – duplas de números primos separados por uma distância de dois. Outra conjectura muito conhecida, chamada conjectura de Goldbach, estabelece que todo número par maior que 2 pode ser escrito como a soma de dois números primos. Por exemplo, 16 = 13 + 3; 54 = 47 + 7. Se você conseguir provar qualquer uma dessas conjecturas, ganhará fama imortal.3
Sem dúvida, em matemática, o problema não resolvido mais famoso é a chamada hipótese de Riemann, proposta pelo mesmo Bernhard Riemann já mencionado. Em seu único artigo de pesquisa sobre os números primos, publicado em 1859, Riemann propôs uma hipótese que prevê até onde o verdadeiro valor de Π(x), a quantidade de primos até x, é a aproximação dada pelo teorema dos números primos. Em outras palavras, o que se pode dizer do “termo erro” no teorema dos números primos: a diferença entre a quantidade real e a fórmula sugerida? A Clay Foundation considera esse um dos sete problemas para cuja solução pagará um prêmio de 1.000.000 de dólares! Se até agora você não se interessou pelo assunto, talvez essa bolada o motive…
Por que isso é importante? A quem interessa? Os matemáticos avaliam seus problemas, sobretudo, pela dificuldade e beleza intrínseca. O dos números primos atende como poucos a esses critérios. No entanto, os números primos são também úteis na prática. Sua pesquisa encontrou um emprego importante na criptografia (a ciência de codificar mensagens secretas) nas últimas décadas. Já mencionamos o livro de ficção de Carl Sagan sobre uma cultura extraterrestre que se comunica com a humanidade por meio de números primos. Mas existe uma área bem mais “quente”, em nada fictícia, que usa os números primos para propósitos tanto civis quanto militares: as transmissões codificadas.
Quando tiramos dinheiro em um caixa eletrônico, usamos um cartão de débito e a comunicação entre nós e o caixa é codificada. Como muitos outros códigos para criptografia, o que está em todo cartão de débito, chamado RSA (em alusão a seus inventores, Rivest, Shamir e Adleman), se baseia nas propriedades dos números primos.
A história dos números primos ainda é rodeada de mistério. Essa história ainda não terminou…
Glossário
Número composto: Número inteiro que pode ser escrito como produto de dois números menores. Por exemplo, 24 = 3 x 8.
Número primo (não composto): Número inteiro que não pode ser escrito como produto de dois números menores, como 7 ou 23.
Prova matemática: Série de argumentos lógicos cujo propósito é demonstrar a verdade de um teorema matemático. A prova decorre de pressupostos básicos que foram testados ou de outros teoremas provados anteriormente.
Teorema matemático: Proposição expressa em linguagem matemática que, em definitivo, pode ser declarada válida ou inválida dentro de determinado sistema.
Conjectura matemática (ou hipótese): Asserção matemática tida como verdadeira, mas ainda não provada. A “crença na validade” pode resultar do exame de casos especiais, da evidência computacional ou da intuição matemática. Existem conjecturas matemáticas a respeito das quais não há concordância.
Números primos gêmeos: Dupla de números primos com diferença de dois entre si, como 5, 7 ou 41, 43.
Leituras adicionais
[1] Du Sautoy, M. 2003. The Music of the Primes. HarperCollins.
[2] Doxiadis, A. 1992. Uncle Petros and Golbach’s Conjecture. Bloomsbury.
[3] Pomerance, C. 2004. “Prime numbers and the search for extraterrestrial intelligence”, em Mathematical Adventures for Students and Amateurs, D. Hayes e T. Shubin, orgs. (M.A.A.), 1–4.[4] ↑ Singh, S. 1999. The Code Book. London, Fourth Estate.
Notas
[1] A divisão do círculo em 360 graus aparece pela primeira vez nos escritos de astrônomos egípcios e gregos, mas se baseia na antiga divisão da hora em 60 minutos pelos babilônios. Sem dúvida, está relacionada também ao fato de o ano solar ter 365 dias (em média); observe, porém, que 365 = 5 x 73 e, como tanto 5 quanto 73 são primos, 365 admite menos fatorações que 360.
[2] A leitura correta de um texto matemático é uma “leitura ativa”, pela qual o leitor avalia o que está sendo dito, os exemplos de computador, etc. Mas, se você quiser saltar a tarefa proposta, pode fazer isso, pois voltaremos a ela e a discutiremos mais tarde.
[3] A conjectura dos números primos gêmeos teve impressionantes progressos ultimamente, devidos a Zhang e Maynard, mas mesmo assim continua em aberto. No tocante à conjectura de Goldbach, Helfgott provou em 2014 que todo número ímpar maior que 5 é a soma de três primos.
Citação
de Shalit, E. (2018). “Prime numbers – why are they so exciting?” Front. Young Minds. 6:40. DOI: 10.3389/frym.2018.00040.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br