Por que estudar populações animais?

Os cientistas precisam coletar informações para descobrir uma maneira de proteger o ambiente e os animais que nele vivem. Às vezes, recorrem à matemática para testar teorias que levantaram a respeito dos animais ou mesmo para predizer o futuro! Isso é chamado de modelagem matemática. Modelar as relações entre predadores e presas ajuda os cientistas a compreender por que suas populações mudam com o tempo e a detectar se determinado animal corre o risco de extinção. Para elaborar um modelo matemático adequado, precisamos coletar dados do ambiente. Neste artigo, mostraremos como um pouco de matemática básica (por exemplo, soma, subtração e multiplicação) pode ser usada para modelar as relações entre predador e presa tais como acontecem existem no ambiente selvagem.

Primeiro, precisamos de dados!

Bons modelos começam com bons dados. A fim de modelar uma relação predador-presa, utilizaremos dados populacionais (registros do número de animais existentes) coletados por uma empresa que caçava tanto predadores quanto presas por causa de seu pelo, nos séculos 19 e 20. A antiga empresa Companhia da Baía Hudson fazia registros do número de peles de linces e lebres que caçava. A Figura 1 mostra os dados da empresa para o número de peles de linces e de lebres, que nos revela os níveis da população de cada animal e nos fornece um quadro razoável da relação predador-presa. Os dados mostram que em alguns anos, como 1927, havia mais linces (predadores) e menos lebres (presas), ao passo que em outros, como 1932, havia mais lebres e menos linces.

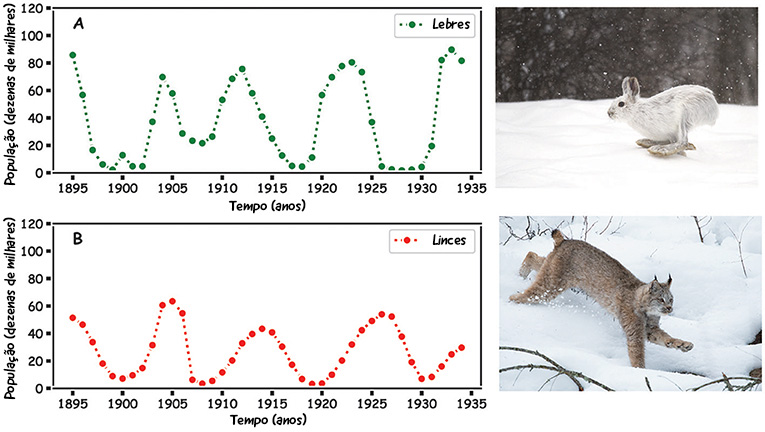
O que nos dizem os dados da Companhia da Baía Hudson?

O aumento e a diminuição das populações registradas de lebres e linces ao longo do tempo sugerem que existe uma relação entre os dois animais – o que faz sentido, pois sabemos que linces comem lebres. Na Figura 1, você percebe que ambas as populações aumentam e diminuem mais ou menos ao mesmo tempo? Quando há mais linces, eles comem mais lebres; a população de lebres diminui, restando menos alimento para os linces, cuja população, por sua vez, diminui. Quando a população de linces diminui, a das lebres volta a aumentar e o ciclo de aumento e diminuição continua. Se as populações de predadores e presas se equilibram, a caça dá sequência ao processo de aumento e diminuição ao longo do tempo, e o círculo da vida prossegue. A pergunta que um matemático faz é: “Posso explicar esse fato usando soma, subtração e multiplicação a fim de calcular as populações futuras?”

Como explicar a relação com modelos matemáticos?

Os matemáticos usam equações diferenciais e dados para descrever o que veem no mundo. A relação predador-presa foi descrita pela primeira vez, com o uso de equações diferenciais, por dois cientistas chamados Lotka [1] e Volterra [2]. Eles empregaram a matemática para explicar o aumento e a diminuição observados na relação geral entre predador e presa.

As equações podem às vezes parecer muito complicadas, mas conseguem descrever como e por que as populações se alteram. Um matemático famoso, chamado Leonhard Euler (1707-1783), mostrou que as equações diferenciais podiam ser escritas como valores de mais e de menos, com um pouquinho de multiplicação. As equações diferenciais podem ser usadas para modelar as populações de linces (predadores) e lebres (presas) aproveitando-se os dados da Companhia da Baía Hudson. Ajustamos os dados originais recorrendo a métodos matemáticos [3] a fim de estimar os valores para a taxa de crescimento (^tcrescimento), a taxa de morte (^tmorte), a taxa comida (^tcomida) e a taxa de alimento (^talimento), que usaremos para predizer as populações de lebres e linces.

Modelagem da população de lebres

Ao desenvolver uma equação, o matemático pensa no mundo. Agora, pensemos no que acontece com a população de lebres ao longo do tempo. Se não houver linces, então a população de lebres no futuro, L_F, será igual à população de lebres atual, L_A, mais nascimentos e menos mortes. A isso chamamos de taxa de crescimento, ^rcrescimento. O número de nascimentos e mortes dependerá do número de lebres vivas no momento; então, multiplicamos ^rcrescimento por L_A (Figura 2A).

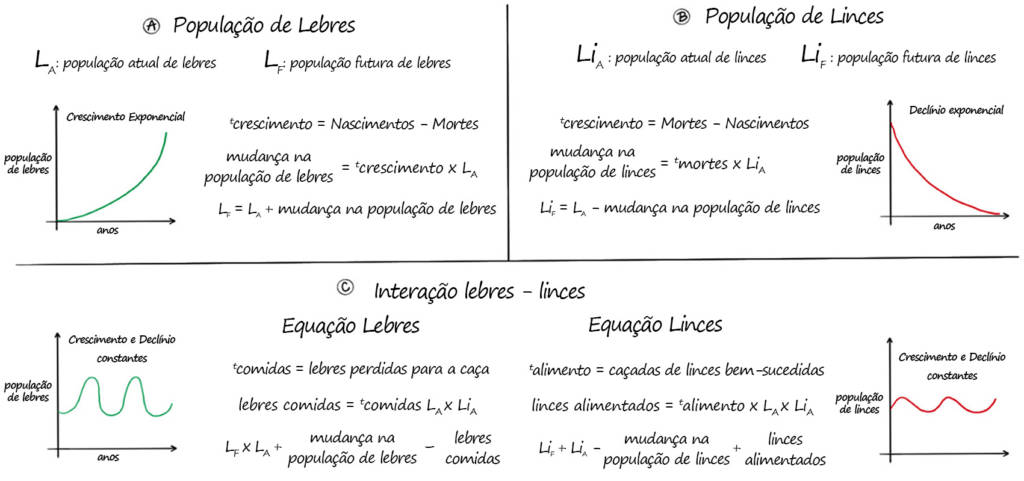
Usemos os dados da Companhia da Baía Hudson para inserir números na equação. Quando os dados começaram a ser colhidos, em 1895, a população de lebres era de 85; portanto, seja L_A = 85 lebres. A taxa de crescimento para a população de lebres é ^tcrescimento  = 0,9 em um ano. Como ^tcrescimento é positivo, esperamos que a população futura aumente. Assim, em 1896, a população futura de lebres, L_F, será:

L_F = L_A + (^tcrescimento x L_A), L_F = 85 + (0,9 x 85) = 161,5.

Previmos que a população futura de lebres será de 165,5 lebres. Se a população continuar crescendo assim, o mundo inteiro ficará coberto de lebres, fenômeno a que se dá o nome de crescimento exponencial (Figura 2A).

Modelagem da população de linces

Consideremos o que acontece à população de linces ao longo do tempo. Se não houver lebres, os linces não terão alimento e sua população diminuirá. Para modelar esse fenômeno, usamos a subtração. O número futuro de linces (Li_F) é igual ao número atual (Li_A) menos a taxa de mortes, ^tmortes, vezes o número atual (Figura 2B).

A população de linces, em 1895, é 51; e, aplicando os dados, estabelecemos a taxa de mortes em ^tmortes = 0,25. A equação então será:

Li_F = L_A – (^tmortes x Li_A),

Li_F = 51 – (0,25 x 51) = 38,25.

Portanto, segundo nossos cálculos, a população futura de linces será, em 1896, de 38,25 linces. Isso se chama declínio exponencial e, se continuar acontecendo, não haverá mais linces (Figura 2B).

Modelagem da interação lebres-linces

Por si mesma, a população de lebres aumenta enquanto a de linces diminui. Como saber de que modo essas populações interagem? Linces comem lebres e, assim, fazem com que a população destas diminua; assim, usamos a subtração para modelar esse fenômeno. Precisamos de um termo para a taxa de lebres comidas, ^tcomidas, que depende da população atual de linces e da população disponível de lebres, para que aqueles comam e estas sejam comidas. Portanto, multiplicamos ^tcomidas por Li_A  e L_A.

Seguindo a mesma lógica, as lebres são uma fonte de alimento para os linces; então, empregamos a soma na equação dos linces e multiplicamos a população atual de lebres pela população atual de linces vezes uma taxa de alimento, ^talimento (Figura 2C).

Os valores de L_A = 85 lebres, ^tcrescimento = 0,9, Li_A  =  51 linces, e a ^tmortes = 0,25 permanece a mesma. Com base nos dados, obtemos uma taxa de lebres comidas de ^tcomidas = 0,024 e uma taxa de alimento de ^talimento = 0,005. Inserindo esses dados na equação de predição do número futuro de lebres, obtemos:

L_F  = L_A + (^tcrescimento x L_A) – (^tcomidas x Li_A x L_A),

L_F  = 85 + (0,9 x 85) – (0,024 x 85 x 51) = 59,24,

e a equação da predição do número futuro de linces dará:

Li_F = Li_A – (^tmortes x Li_A) + (^talimento x Li_A x L_A),

Li_F = 51 – (0,25 x 51) + (0,005 x 51 x 85) = 59,925.

Nosso modelo (as duas equações acima) prediz um declínio na população de lebres e um aumento na população de linces em 1895, conforme mostrado na Figura 3 pelas setas verde e vermelha.

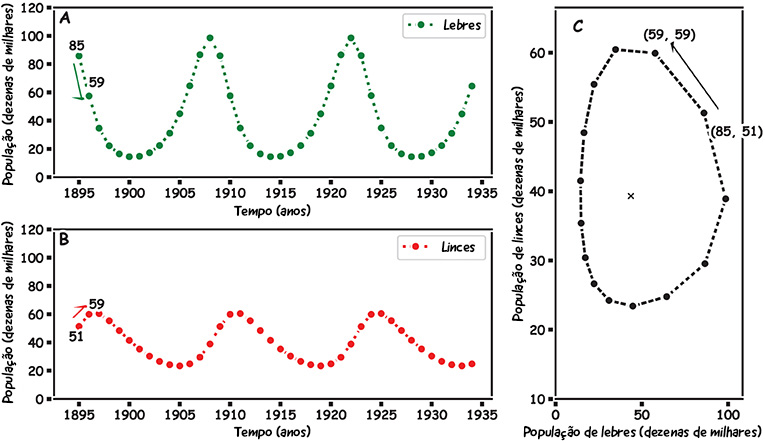
A fim de predizer como as populações mudarão no ano seguinte, 1897, aplicaremos nossos valores L_F e Li_F a L_A  e Li_A nas novas equações. Toda vez que fizermos isso, obteremos novos valores e cada valor será um ponto em nossos gráficos da Figura 3.

Visualização da relação predador-presa

Usando as equações acima e alguns códigos de computador [4], simulamos as populações de linces e lebres, fazendo com que nossos dados mostrem como a relação predador-presa evolui com o tempo (Figura 3).

Outra maneira de mostrar como duas espécies estão associadas é simular de que maneira a população de lebres (eixo x) e a população de linces (eixe Y) mudam em sua relação mútua (Figura 3C). O x no meio mostra a média das populações de lebres (39) e de linces (45), sendo conhecido como ponto de equilíbrio. As populações de linces e lebres orbitam em torno dessa média enquanto as populações aumentam e diminuem, formando o círculo da vida. Isso lembra a órbita da Terra em volta do Sol. As populações giram e giram, o que representa seus pontos altos e baixos ao longo do tempo. Num sistema equilibrado, como o que aqui modelamos, a órbita permanece estável; mas, caso comece a variar para dentro ou para fora, isso pode ser um sinal inicial de mudança.

Uma dessas mudanças ocorreu em 1995, quando lobos foram reintroduzidos no parque Yellowstone. Isso levou a alguns resultados surpreendentes para o ecossistema local³. Com base nessas curiosas observações e na matemática similar à que mostramos aqui, Goodman et al. Desenvolveram um jogo de computador capaz de construir um ecossistema equilibrado⁴.

Os modelos não são exatos

Quando tentam descrever uma coisa complicada, os matemáticos simplificam o procedimento. As equações que mostramos são para simplificá-lo, também. Simplificações são feitas para mostrar que predições e simulações não seguem perfeitamente os dados originais. Eis algumas informações que deixamos de fora de nosso modelo:

. Há mais de um predador para a lebre.

. Os linces não caçam apenas lebres; também comem peixes e esquilos.

. Em nosso modelo, as lebres não ficam sem alimento, o que não é verdade no inverno.

. Que dizer dos caçadores de peles que caçam tanto linces quanto lebres?

Para fazer com que as equações funcionem nessas outras situações, precisaremos incluir outras, além de mais somas e subtrações. Se tivermos todos os dados, poderemos perfeitamente modelar o futuro. Mas mesmo com essas simplificações, os matemáticos ainda conseguem fazer um bom trabalho ao modelar as populações de lebres e linces.

De que outra maneira esse modelo pode ser usado?

Se você trocar “lince” por “tubarão” e “lebre” por “peixe” nesse modelo, a matemática continuará funcionando, com os dados certos [2]. Você poderá até usar as mesmas equações caso troque “lince” por “zumbi” e “lebre” por “humano”! A relação predador-presa pode ser expandida para além das populações animais e usada para modelar a interação entre empresas, as reações químicas e a disseminação dos vírus.

Sumário

A fim de desenvolver modelos do mundo real, os matemáticos precisam, primeiro, ter bons dados. Ou seja, é vital para os cientistas, conservacionistas – e mesmo caçadores de peles! – coletar informação do ambiente. Utilizando dados, podemos visualizar padrões nas relações e depois empregar a matemática para recriar esses padrões e predizer dados futuros que possam representar e predizer o futuro dessas relações. As predições nos ajudam a preservar ecossistemas equilibrados. Felizmente, lendo este artigo, você constata que isso só exige a matemática básica da soma, subtração e multiplicação – e um pouquinho de pensamento inteligente – para modelar e predizer as populações de predadores, presas e muito mais.

Glossário

Equações diferenciais: ↑ Equações que descrevem como as populações mudam com o tempo e muitos outros processos, incluindo como um helicóptero voa, como os planetas orbitam uma estrela ou como o sangue flui por nossas veias.

Estimativa: Valor suficientemente próximo da resposta exata, usualmente obtido com base em algum conhecimento do sistema ou em um cálculo.

Taxa de crescimento: Taxa de crescimento é o aumento da população de lebres quando elas não têm predadores. Pode ser avaliada a partir de dados baseados no número de nascimento menos o número de mortes.

Taxa de mortes: Taxa de mortes é a diminuição da população de linces com o tempo, quando eles não têm o que comer. É o número de mortes menos o de nascimentos.

Taxa de comida: Taxa de comida é o número de lebres caçadas e comidas pelos linces.

Taxa de alimento: Taxa de alimento é o número de lebres que o lince precisa comer para sobreviver.

Crescimento exponencial: Crescimento contínuo e rápido.

Ponto de equilíbrio: Ponto de equilíbrio entre duas populações. Quando um sistema está em equilíbrio, dizemos que é estável.

Agradecimentos

Este trabalho contou com o apoio do Irish Research Council (GOIPG/2020/943).

Referências

[1]  Lotka, A. J. 1920. “Analytical note on certain rhythmic relations in organic systems.” Proc. Natl. Acad. Sci. USA. 6:410–5.

[2] Volterra, V. 1926. “Fluctuations in the abundance of a species considered mathematically.” Nature. 118:558–60.

[3] de Silva, B. M., Champion, K., Quade, M., Loiseau, J. C., Kutz, J. N. e Brunton, S. L. 2020. “PySINDy: a python package for the sparse identification of nonlinear dynamics from data.” arXiv Preprint arXiv: 2004.08424.

[4] Butler, J. S. e Brady, R. M. 2020. Predator Prey Code for Young-Minds. GitHub. Disponível online em https://github.com/john-s-butler-dit/Predator-Prey-for-Young-Minds.

Citação

Brady, R. e Butler, J. (2021). “The circle of life: the mathematics of predator-prey relationships.” Front. Young Minds. 9:651131. DOI: 10.3389/frym.2021.651131.

Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.