O conceito de infinito e seu uso na matemática
Autores
Jovens revisores

Resumo
Você já brincou de dizer o maior número que consegue imaginar? Alguém logo diz: “Infinito”; e o seguinte diz: “Infinito mais um”. O jogo parece nunca acabar. No entanto, o infinito mais um é realmente maior que o infinito? Podemos fazer matemática dentro do infinito? Georg Cantor (1845-1918) foi um dos primeiros matemáticos a estudar o infinito. Ele forneceu vários exemplos de infinito na matemática. Descobriu também que existem diferentes tipos de infinito, o que levou muitos de seus colegas a considerar seu trabalho errado e confuso. Foi David Hilbert quem tornou o infinito inteligível com seu “Hotel do Infinito”, em 1924. É a história de um hotel que, mesmo lotado, tem espaço para mais hóspedes. O presente artigo tenta explicar o infinito de um modo similar.
Introdução: a cardinalidade, isto é, contagem
O infinito é estranho e, para começar, confunde os matemáticos. Ele dá o ar da graça naturalmente quando, pela primeira vez, aprendemos que a contagem não tem limite. Para nos ajudar a entender o estranho comportamento do infinito, os matemáticos voltam ao básico e tentam definir o que significa contar.
Imagine-se com um saquinho de doces. Não pode ver dentro dele, mas quer saber quantos doces há lá. O melhor a fazer é enfiar a mão no saquinho, tirar o primeiro e dizer “um”; depois, tirar o segundo e dizer “dois” e continuar fazendo isso até esvaziar o saquinho. O último número que disser é a quantidade de doces que o saquinho contém. É assim que você aprende a contar, não importa que objetos estejam no saquinho.
Definição de cardinalidade
A cardinalidade de um saquinho de objetos1 é o número de objetos que ali estão. Pode ser determinada pela contagem deles.
Por exemplo, um saquinho com três doces tem cardinalidade três. Um saquinho com um doce, um brinquedo e um lápis também tem cardinalidade três. Não importa o que sejam os objetos, só a quantidade importa. O saquinho poderia conter mesmo objetos abstratos, como os números 1, 2 e 3.
Dois saquinhos com a mesma cardinalidade contêm o mesmo número de objetos. Podemos comparar os objetos dos dois saquinhos sem que em nenhum deles sobre nada. Isso nos propicia outra maneira de contar objetos. Se sabemos a cardinalidade de um saquinho, mas não a do outro, podemos comparar a quantidade de objetos que há nos dois. Por exemplo, você tem um saquinho de doces, mas não sabe quantos doces são. Dessa vez, está com oito amigos. Se der apenas um doce a cada um desses amigos, sem que reste nenhum doce, então a cardinalidade do saquinho de doces é oito. Se um amigo ficar sem seu doce, então a cardinalidade do saquinho é menor que oito. Se sobrar um doce, então a cardinalidade do saquinho é maior que oito.
Infinito contável
Agora, imagine um saquinho contendo todos os números positivos: 1, 2, 3, 4, 5, etc. Usamos o símbolo N para designar esse saquinho2. Qual é a cardinalidade dele? Obviamente, não pode ser 4, pois N contém pelo menos cinco objetos, isto é, os números 1, 2, 3, 4 e 5. A mesma lógica se aplica a qualquer número. Tome um número, por exemplo, n; então, o saquinho N contém os números 1, 2, 3…, n e n + 1. Isso mostra que a cardinalidade de N não é um número; dizemos, então, que N é um infinito contável3.
Definição: infinito contável
Um saquinho de objetos é um infinito contável quando tem a mesma cardinalidade de N. Ou seja:
1. O saquinho contém uma quantidade infinita de objetos, de modo que sempre poderemos tirar alguma coisa dele.
2. Podemos emparelhar cada objeto do saquinho com um número inteiro positivo único (outra forma de dizer: podemos contar os objetos).
Exemplo 1: Números pares
Imagine dois saquinhos. Um com todos os números positivos, chamado N, e o outro com todos os números positivos pares, chamado 2N. Poderia parecer natural pensar que existem mais números positivos do que números positivos pares. Mas mostraremos que você pode emparelhar cada número par exatamente com outro número, de modo a não sobrar nada. Isso revelará que N e 2N possuem a mesma cardinalidade.
Antes de fazer isso, precisamos de um meio de distinguir os números que pegamos do saquinho N dos números pares que pegamos do saquinho 2N e acrescentar º ao final de cada número proveniente do saquinho N.
Exemplos:
. 6º é um número de N e 6 é um número par de 2N
. 7º é um número de N e, como 7 não é par, não está em nosso saquinho 2N.
O modo de emparelhar os números de N e 2N é dizer: o número nº emparelha com o número par 2n. Exemplos:
. O número 4º se emparelha com o número par 8.
. O número 5º se emparelha com o número par 10.
. O número 57º se emparelha com o número par 114.
Como vemos, todo número de N se emparelha com um número par. Vemos também que todo número par se emparelha com outro número, assim como o número par n se emparelha com o número (n ꞉ 2)º. Isso significa que emparelhamos todo número em N com um número em 2N, sem sobras (Figura 1). Portanto, N e 2N têm a mesma cardinalidade. O saquinho com números pares é um infinito contável, isto é, a quantidade de números positivos e de números pares positivos é a mesma.
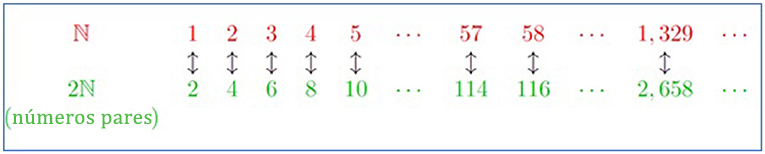
Figura 1. Cada número de N pode ser emparelhado com um único número par de 2N. Portanto, a quantidade de números e de números pares é a mesma.
Acrescentando um ao infinito
Exemplo 2: Imagine dois saquinhos, ambos contendo todos os números positivos. Eles contêm o mesmo número de objetos (são infinitos contáveis). Agora, acrescente um objeto, a letra A, ao segundo saquinho. Será que o segundo saquinho possui mais objetos do que o primeiro? Não, na verdade os dois contêm o mesmo número de objetos.
Como antes, chamaremos o primeiro saquinho de N e acrescentaremos “º” ao final de cada número que há nele. O segundo saquinho, que contém A, 1, 2, 3, etc., chamaremos de N0. Vamos então emparelhar cada objeto em N com um único objeto em N0 usando as duas regras.
[1] O número 1º é emparelhado com a letra A de N0.
[2] Quando n não é um, o número nº é emparelhado com o número n – 1 de N0.
Exemplos:
. O número 1º é emparelhado com a letra A.
. O número 5º é emparelhado com o número 4.
. O número 30º é emparelhado com o número 29.
Assim, todo objeto em N é emparelhado com um único objeto em N0. Portanto, ambos os saquinhos possuem a mesma cardinalidade e, consequentemente, o mesmo número de objetos.
Essa lógica se aplica a qualquer quantidade de coisas que adicionarmos ao saquinho N, de modo que, não importa quantas coisas finitas juntarmos a N, o saquinho continuará um infinito contável e conterá o mesmo número de objetos.
Adicionando infinito ao infinito
Exemplo 3: Vimos que um saquinho com todos os números positivos é um infinito contável. Pela mesma lógica, um saquinho com todos os números negativos também é um infinito contável. E se pusermos, em um saquinho, todos os números positivos, todos os números negativos e 0? Esse saquinho é maior que o saquinho N?
Usaremos o símbolo ℤ para significar o saquinho que contém todos os números (positivos, negativos e zero)4. Para emparelhar os números em N com os números em ℤ, precisamos empregar regras mais complicadas.
1. Se n for ímpar, então nº é emparelhado com (n – 1) : 2 em ℤ.
2. Se n for par, então nº é emparelhado com – (n : 2) em ℤ.
Exemplos:
. 4 é par e 4 : 2 = 2. Portanto, o número 4º é emparelhado com o número –2.
. 5 é ímpar, portanto calculamos 5 – 1 = 4 e 4 : 2 = 2. Portanto, o número 5º é emparelhado com o número 2.
. O número 24º é emparelhado com o número – 12.
. O número 57º é emparelhado com o número 28.
De novo, emparelhamos cada objeto em N com um objeto em ℤ (Figura 2). Ou seja, ambos têm a mesma cardinalidade. Assim, ℤ é contavelmente infinito. A quantidade de números (positivos e negativos) e de números positivos é a mesma.

Figura 2. Cada número de N pode ser emparelhado com um único número de ℤ. Portanto, a quantidade de números e de números positivos e negativos é a mesma.
Subtraindo do infinito
Vimos que acrescentar um objeto ou uma quantidade infinita de objetos a um saquinho contavelmente infinito não torna esse saquinho maior (Exemplo 3). Mas o que acontecerá se começarmos a remover objetos de um saquinho contavelmente infinito?
Exemplo 4: Imagine um saquinho que contenha todos os números positivos e remova dele o número 1. Chamaremos esse saquinho de N1. Mostramos que o saquinho N1 é contavelmente infinito emparelhando cada elemento de N1 com um elemento de N. Como antes, acrescentaremos “º” ao final de cada número proveniente de N. Emparelharemos o número nº (de N) com o número n + 1 de N1.
Exemplos:
. O número 1º é emparelhado com o número 2.
. O número 5º é emparelhado com o número 6.
. O número 30º é emparelhado com o número 31.
Todo objeto em N é emparelhado com um único objeto em N1. Portanto, ambos os saquinhos possuem a mesma cardinalidade e, consequentemente, o mesmo número de objetos.
Essa lógica se aplica a qualquer quantidade de coisas que removermos do saquinho N. Não importa a quantidade de coisas finitas que removermos de N, o saquinho continuará contavelmente infinito e conterá a mesma quantidade de objetos.
E se removermos uma quantidade infinita de objetos contáveis? Então, a resposta dependerá do que removermos.
Exemplo 5: Sabemos que os números positivos pares são contavelmente infinitos (Exemplo 1). Imagine um saquinho com todos os números positivos e remova dele todos os números positivos pares. Só restarão no saquinho os números positivos ímpares. Assim como os números pares são contavelmente infinitos, os números ímpares também o são (para constatarmos isso, emparelhamos o número nº com o número 2n – 1 número ímpar, ver Figura 3).

Figura 3. Cada número de N pode ser emparelhado com um único número ímpar. Assim, a quantidade de números e números ímpares é a mesma.
Nesse caso, começando com um saquinho contavelmente infinito e removendo dele objetos contavelmente infinitos, ainda ficamos com uma quantidade infinita de objetos contáveis ou, em outras palavras, com um saquinho contavelmente infinito.
Exemplo 6: Imagine um saquinho com todos os números positivos, como o saquinho N. Então, removemos todos os números maiores que 1. O que removemos de N é o saquinho N1 (Exemplo 4). Ficamos com um saquinho que contém o número 1. O saquinho que contém apenas o número 1 tem cardinalidade 1.
Nesse caso, começando com um saquinho contavelmente infinito e removendo dele objetos contavelmente infinitos, ficamos com um único objeto.
Conclusão
Este artigo mostra alguns dos estranhos comportamentos do infinito. Os exemplos acima revelam que não podemos trabalhar com o infinito como se ele fosse um número. Quando fazemos adição ou subtração, o infinito se comporta diferentemente dos números.
Essa estranheza confundiu os matemáticos a princípio, mas eles conseguiram por fim, voltando ao básico, entender o infinito. Ao longo da história, vem sendo repetido que conceitos outrora misteriosos foram finalmente compreendidos depois que se tratou com cuidado a definição.
Glossário
Cardinalidade: O número de objetos em um saquinho.
N: Os “números naturais”, o saquinho que contém todos os números positivos, 1, 2, 3, 4, etc.
Infinito contável: Um saquinho que contém objetos em quantidade infinita, mas mesmo assim contáveis. Ou seja, um saquinho com a mesma cardinalidade que N.
ℤ: Os “inteiros”, o saquinho que contém todos os números negativos, zero e todos os números positivos.
Notas
1. Em matemática, usamos a palavra “conjunto” para significar um saquinho de objetos.
2. N é um N em negrito. Significa “números naturais”.
3. Usamos o advérbio “contavelmente” porque existem outros tipos de infinito, infinitamente maiores que infinitos contáveis.
4. Trata-se de um Z em negrito e significa Zahlen, a palavra alemã para “números”.
Citação
Bouyer, F. (2018). “Infinity and Trying To Do Maths With It.” Front. Young Minds. 6:61. DOI: 10.3389/frym.2018.00061.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br