O paradoxo do tempo de espera
Autores
Jovens revisores

Resumo
Suponha que você esteja indo para a escola e pare em um ponto de ônibus. Quanto tempo terá de esperar antes que o próximo ônibus chegue? Surpreendentemente, será um tempo mais longo – possivelmente muito mais longo – do que você imaginou ao consultar a tabela de horários. Esse fenômeno, chamado de paradoxo do tempo de espera, tem origem puramente matemática. Neste artigo, exploramos o paradoxo do tempo de espera, explicamos por que ele ocorre e discutimos algumas de suas implicações (além da possibilidade de se chegar atrasado à escola).
Quanto tempo você tem de esperar pelo próximo ônibus?
Suponha que, em sua cidade, você precise pegar um ônibus para ir à escola. Como os ônibus estão sempre passando por seu bairro, talvez você não precise prestar muita atenção aos horários. Talvez apenas vá até o ponto mais próximo e pegue o próximo que passar (veja a Figura 1A). No entanto, se você chegar e não tiver ideia de quando virá o próximo ônibus, quanto tempo terá de esperar por ele?
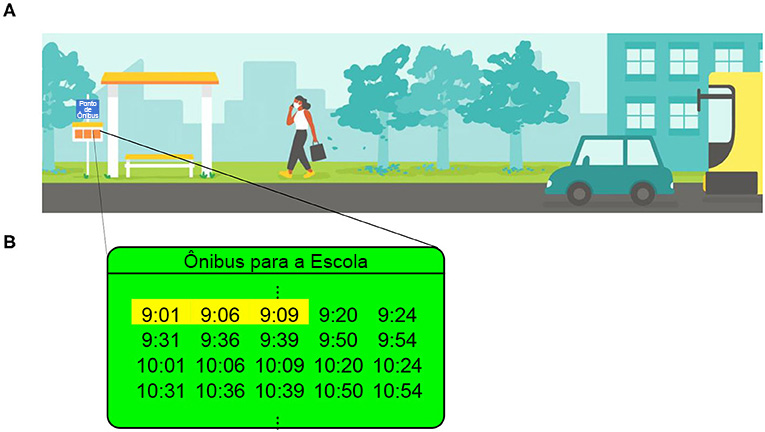
Supondo-se que dez ônibus passem a cada hora (veja a Figura 1B), então um ônibus passa a cada 6 minutos em média. Se o ônibus mais recente sair logo antes de você chegar, talvez seja necessário esperar 5 ou 6 minutos pelo próximo. Se o ônibus mais recente sair uns minutos antes de você chegar, talvez o próximo chegue em apenas 1 minuto. Ou quatro? Ou cinco? Um palpite para o seu “tempo de espera” é de 3 minutos, que é metade do tempo entre os ônibus, em média. No entanto, esse raciocínio é incorreto. Em geral, você tem de esperar mais que 3 minutos. Seu tempo de espera pode ser ainda maior do que 6 minutos e esse fenômeno é chamado de paradoxo do tempo de espera [1, 2].
Um paradoxo é algo que parece não fazer sentido, mas na verdade acaba sendo correto. Muitas pessoas pensam no tempo de espera como um paradoxo porque um tempo de espera típico em uma rodoviária é maior do que a metade do intervalo médio de tempo entre os ônibus (que é de 3 minutos no exemplo acima). O paradoxo do tempo de espera é um fenômeno matemático e não diz respeito a ônibus. O que vem a ser esse fenômeno e como ele nos engana? Continue lendo para descobrir!
Por que o paradoxo do tempo de espera ocorre?
Para entender por que o paradoxo de tempo de espera ocorre, considere os horários de ônibus na Figura 2A. Nessa tabela, mais simples que a da Figura 1, os ônibus chegam em intervalos de 4 ou 12 minutos. A tabela original na Figura 1B tem vários números de aparência irregular e vários intervalos diferentes entre as chegadas dos ônibus. Em geral, quando uma situação parece complicada, é útil simplificá-la antes de aplicar o raciocínio matemático. Pessoas que trabalham com matemática fazem isso o tempo todo. O paradoxo do tempo de espera também ocorre na tabela simplificada dos ônibus e a simplificação facilita o entendimento do que está acontecendo.
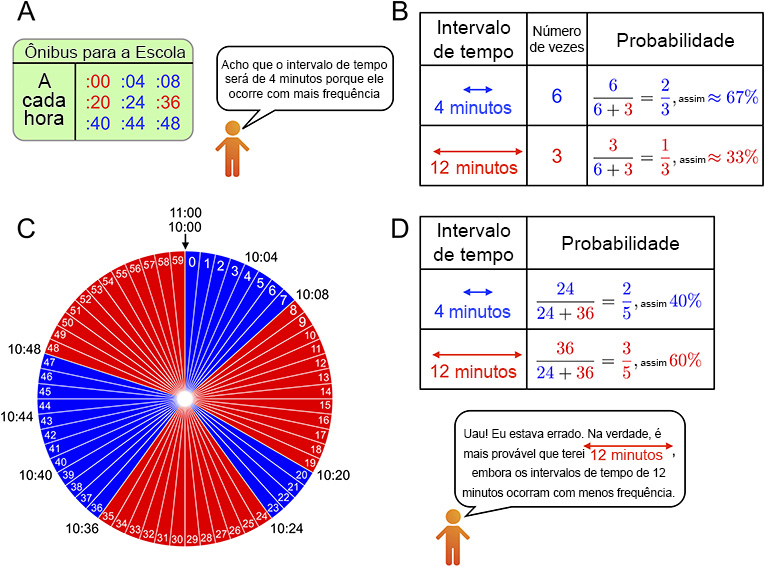
(A) Uma tabela de horários de ônibus simplificada. (B) Palpite sobre as probabilidades de obter tempos entre eventos de 4 e 12 minutos. Essa suposição é baseada na ideia incorreta de que um tempo entre os eventos de 4 minutos é mais provável do que um de 12 minutos porque ocorre mais frequentemente. (C) Observar os períodos do intervalo de tempo em uma hora como um gráfico de pizza pode nos ajudar a entender por que isso não é correto. A probabilidade real de obter um tempo entre eventos de 12 minutos é maior do que a probabilidade de obter um de 4 minutos porque há 36 fatias vermelhas, mas apenas 24 fatias azuis no gráfico de pizza em (C).
Um conceito-chave a considerar é o tempo entre os eventos, que é o tempo entre dois ônibus consecutivos. A tabela da Figura 2A indica que, a cada hora, seis ônibus chegam imediatamente após um tempo entre eventos de 4 minutos (azul) e três ônibus chegam imediatamente após um tempo entre eventos de 12 minutos (vermelho). Em nosso cenário, lembre-se de que você chegou ao ponto de ônibus sem saber quando o próximo ônibus passaria. Na linguagem da teoria da probabilidade, dizemos que você chega ao ponto de ônibus em um horário uniformemente aleatório. Você acha mais provável um intervalo de 4 ou de 12 minutos entre os eventos? Se o tempo entre eventos for de 4 minutos, não esperará muito pelo próximo ônibus. No entanto, se for de 12 minutos, o tempo de espera poderá ser maior. Como mencionamos acima, seis tempos entre eventos perfazem 4 minutos e três tempos perfazem 12.
Pense desta forma: talvez seja provável que você obtenha um tempo entre eventos de 4 minutos porque há seis deles a cada hora, mas os tempos entre eventos de 12 minutos ocorrem apenas três vezes a cada hora. O primeiro ocorre com uma probabilidade de 6/(6+3) = 2/3, que é cerca de 0,67, então essa situação ocorre cerca de 67% das vezes (Ver Figura 2B). O último ocorre com uma probabilidade de 3/(6+3) = 1/3, consequentemente cerca de 33% das vezes.
Infelizmente, isso é uma racionalização de desejo. Chegar a um ponto de ônibus uniformemente aleatório é como girar uma roda com os números de 0 a 59 em cada “fatia” da roda (portanto, há 60 fatias no total), pará-la com o dedo e olhar para a fatia que seu dedo está tocando. Se o seu dedo apontar para 33, significa que você chegou ao ponto às 10:33 h. Nesse caso, você precisa esperar 3 minutos pelo próximo ônibus, que chegará às 10:36 h. A roda nos ajuda a entender a noção de “uniformemente aleatório”. Cada minuto na roda é colorido, com o azul correspondendo a um tempo entre eventos de 4 minutos e o vermelho a um tempo de 12 minutos. Na Figura 2C, vemos que há 24 minutos azuis e 36 minutos vermelhos.
A partir dessa imagem, também vemos que é mais provável obtermos um tempo entre eventos de 12 minutos (isso ocorre com uma probabilidade de 0,60) do que um de 4 (isso ocorre com uma probabilidade de 0,40) (consulte a Figura 2D).
Embora apenas três dos nove tempos entre eventos (com uma probabilidade de 1/3 de haver um) tenham 12 minutos de duração, ainda é mais provável (especificamente, a probabilidade é de 0,60) que transcorra um desses intervalos do que um intervalo de 4 minutos entre eventos. Por quê? A resposta vem de um fato simples: o tempo longo entre eventos é longo, e o curto é curto. Um tempo longo entre eventos ocupa 12 números de uma roda de jogo, mas um curto ocupa apenas 4 números. Os três longos tempos entre eventos, juntos, cobrem 12 x 3 = 36 dos 60 minutos. Em contraste, os seis curtos, juntos, cobrem apenas 4 x 6 = 24 minutos. Consequentemente, a raridade de um tempo entre eventos em uma tabela de horários de ônibus não implica que seja raro encontrar esse tempo.
Fazendo mais alguns cálculos com a tabela de horários de ônibus na Figura 2A, vemos que o palpite sobre o tempo de espera (metade do tempo médio entre eventos) é de 3 minutos e 20 segundos, mas o tempo médio real de espera é de 4 minutos e 24 segundos. No cronograma da Figura 1B, o palpite para o tempo médio de espera é de 3 minutos e o tempo de espera real é, em média, de 3 minutos e 40 segundos. Suponha que todos os tempos entre eventos sejam de 6 minutos, o que significa que os ônibus chegam exatamente a cada 6 minutos. Nesse caso, não há mais um paradoxo do tempo de espera porque a estimativa e o tempo médio real de espera são de 3 minutos. Para que o paradoxo do tempo de espera ocorra, precisamos ter uma mistura de pelo menos dois tempos entre eventos, tais como de 4 e 12 minutos.
Aplicações e extensões
O paradoxo do tempo de espera não se aplica apenas à espera pelo ônibus. Os tempos entre eventos são importantes em muitas situações. Considere o “evento” de conversar com um colega na escola. Os tempos entre eventos são as quantidades de tempo entre as conversas com os colegas (ver Figura 3A). Um tempo entre eventos pode ser de 2 minutos e o próximo de 11 minutos. Nas atividades sociais, ao contrário dos horários dos ônibus, muitas vezes há grandes variações nos horários entre os eventos. Na Figura 3B, mostramos um histograma de tempos entre eventos a um estudante da França [3]. No histograma, listamos os tempos da esquerda para a direita, em ordem crescente. A altura de cada barra no histograma indica o número de vezes que cada tempo entre eventos ocorre. A maioria dos tempos entre eventos é curta (20 ou 40 segundos, por exemplo), mas uns poucos são longos (200 ou 400 segundos).
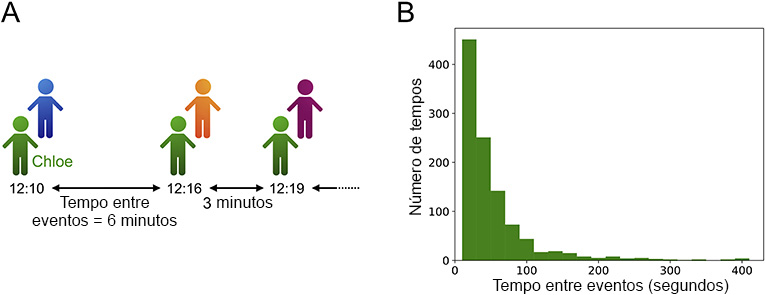
(A) O tempo entre eventos para uma aluna chamado Chloe. Chloe conversa com três diferentes alunos, com tempos entre eventos de 3 e 6 minutos. (B) Um histograma de tempos entre eventos para um aluno em uma escola na França. Esse exemplo vem do conjunto de dados “Primary School” do projeto SocioPatterns [3]. Selecionamos o aluno com maior número de eventos e calculamos todos os seus tempos entre eventos. As barras na figura indicam o número de vezes entre eventos de cada duração para esse aluno. O histograma mostra que há grandes variações nos tempos entre eventos. Muitos são curtos, mas alguns são muito longos.
Em nosso exemplo do paradoxo do tempo de espera de ônibus, vimos que, mesmo havendo apenas três longos tempos entre eventos num total de nove, é mais provável que tenhamos um dos longos do que um dos curtos. Esse é um exemplo de amostragem tendenciosa. Outro exemplo famoso de amostragem tendenciosa é o paradoxo da amizade [4, 5]. De acordo com ele, seus amigos tendem a ter mais amigos do que você. No entanto, não há razão para ficar chateado, porque esse também é um fenômeno puramente matemático. Se você tem 20 amigos em sua escola, muitos deles provavelmente são pessoas populares. Por exemplo, se Alice tiver apenas um amigo, é improvável que você seja o único amigo de Alice; é mais provável que seja outra pessoa. Por outro lado, se Beto é amigo da metade dos alunos de sua escola, é muito provável que você seja um dos amigos de Beto.
Esperar o próximo ônibus e contar o número de amigos pode parecer algo sem conexão. No entanto, do ponto de vista matemático, é provável que você tenha um amigo como Beto basicamente pelo mesmo motivo pelo qual, provavelmente, pegará um ônibus depois de um longo período entre eventos. Suponha que haja seis alunos com quatro amigos cada um e três alunos com doze amigos cada. Se você é amigo de apenas um desses nove alunos, é provável que seu amigo o seja de doze, embora haja apenas três alunos com doze amigos entre os 6 + 3 = 9 alunos. Esses números são exatamente os mesmos que usamos na Figura 2 para demonstrar o paradoxo do tempo de espera. Isso mostra que o paradoxo do tempo de espera e o paradoxo da amizade têm a mesma origem matemática. Ambos são consequências da amostragem tendenciosa.
A compreensão do paradoxo do tempo de espera é útil em muitas situações, como para entender a rapidez com que uma doença se espalha em uma população [6]. Em cursos universitários e pesquisas científicas, o paradoxo do tempo aparece com frequência em tópicos como teoria da probabilidade, teoria das filas e análise de redes. Como vimos, a matemática fornece uma maneira de unificar ideias aparentemente diferentes e de descobrir quando elas estão intimamente relacionadas. Isso é verdade não apenas para o paradoxo do tempo de espera e o paradoxo da amizade, mas também para muitas outras coisas.
Glossário
Paradoxo do tempo de espera: Fenômeno matemático sobre tempos que parece não fazer sentido, mas na verdade é correto. No paradoxo do tempo de espera, se um evento ocorre em um momento que escolhemos uniformemente ao acaso, o tempo médio de espera até o próximo evento é normalmente maior que a metade do tempo entre eventos. O paradoxo do tempo de espera também é chamado de “paradoxo do ônibus” e “paradoxo da inspeção”.
Tempo entre eventos: Quantidade de tempo entre dois eventos consecutivos, como a chegada de dois ônibus a um ponto ou duas conversas de uma pessoa com outras.
Teoria das probabilidades: Parte da matemática que se ocupa de tópicos relacionados à “probabilidade”, isto é, uma descrição numérica de quão provável é que um resultado ocorra. Uma “distribuição de probabilidade” é uma função matemática que fornece as probabilidades de todos os resultados possíveis de alguma ação.
Uniformemente aleatório: Distribuição de probabilidades na qual cada resultado possível tem a mesma probabilidade de ocorrer.
Histograma: Diagrama que mostra as contagens de itens em vários intervalos de números para comparar a contagem dos itens em cada intervalo. Por exemplo, um histograma pode mostrar crianças nas faixas etárias de 0 a 4 anos, 5 a 9 anos, 10 a 14 anos e assim por diante. A altura da barra para a faixa etária de 10 a 14 anos indica o número de pessoas entre 10 e 14 anos.
Amostragem tendenciosa: A amostragem tendenciosa ocorre quando alguém seleciona itens (ou, em linguagem mais técnica, “colhe amostras”), como longos períodos entre eventos ou uma pessoa com muitos amigos, de uma coleção de itens, mais frequentemente que outros itens em resultado das regras da seleção.
Agradecimentos
Agradecemos aos nossos jovens leitores – Nia Chiou, Taryn Chiou, Valerie E. Eng, Anthony Jin, Iris Leung, Maple Leung, Ami Masuda e Ritvik Mukherjee – por seus muitos comentários úteis. Também agradecemos a seus pais e professores – Lyndie Chiou e Christina Chow – por nos colocarem em contato e facilitarem sua ajuda. Agradecemos a Iris Leung por desenhar a Figura 1A. Muitos agradecimentos a nosso líder e organizadores por suas sugestões úteis.
Somos gratos pela colaboração da SocioPatterns (ver http: //www.sociopatterns.org) no fornecimento de dados. O NM reconhece o apoio do AFOSR European Office (número de concessão FA9550-19-1-70240). O MAP agradece o apoio da National Science Foundation (número de concessão 1922952) por meio do programa Algorithms for Threat Detection (ATD).
Referências
[1] Welding, P. I. 1957. “The instability of a close-interval service.” J. Oper. Res. Soc. 8:133–42. DOI: 10.1057/jors.1957.21.
[2] Masuda, N. e Hiraoka, T. 2020. “Waiting-time paradox in 1922.” Northeast J. Complex Syst. 2:1. DOI: 10.22191/nejcs/vol2/iss1/1.
[3] Isella, L., Romano, M., Barrat, A., Cattuto, C., Colizza, V., Van den Broeck, W. et al. 2011. “Close encounters in a pediatric ward: Measuring face-to-face proximity and mixing patterns with wearable sensors.” PLoS ONE 6:e17144. DOI: 10.1371/jornal.pone.0017144.
[4] Feld, S. L. 1991. “Why your friends have more friends than you do.” Am. J. Social. 96:1464–77. DOI: 10.1086/229693.
[5] Strogatz, S. 2012. Friends You Can Count On. The New York Times. Disponível online em: https://opinionator.blogs.nytimes.com/2012/09/17/friends-you-can-count-on/.
[6] Karsai, M., Kivelä, M., Pan, R. K., Kaski. K., Kertész, J., Barabási, A. L. et al. 2011. “Small but slow world: how network topology and burstiness slow down spreading.” Phys. Ver. E 83:025102(R). DOI: 10.1103/PhysRevE. 83.025102.
Citacão
Masuda, N. e Porter, M. (2021). “The Waiting-Time Paradox.” Front. Young Minds. 9:582433. DOI: 10.3389/frym.2020.582433.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br