A professora Ingrid Daubechies recebeu o prêmio Wolf em 2023 por seu trabalho em teoria das wavelets e análise harmônica aplicada.

O impulso matemático

A matemática nos ajuda a descobrir coisas usando apenas o cérebro. Para mim, isso é verdadeiramente mágico. Acho que todos nós temos um impulso matemático porque gostamos de usar o cérebro e de pensar, fazer conexões, chegar a conclusões e verificar se essas conclusões são verdadeiras. Isso é exatamente o que faço em meu trabalho diário como matemático. Tento entender a estrutura das funções matemáticas, desmontando-as e juntando-as novamente. Esse processo de desmontagem e remontagem acontece em muitas outras atividades que também exigem aprendizado. Até mesmo grandes comediantes como Chris Rock fazem isso para melhorar suas atuações, desmembrando piadas de sucesso e usando suas partes para criar outras! Adiante, falarei sobre uma conquista obtida com esse tipo de processo de aprendizagem – uma ferramenta matemática muito útil chamada wavelets. 

O que são wavelets?

Wavelets, também chamadas de ondaletas, são funções matemáticas que nos ajudam a processar e analisar imagens e outros tipos de sinais [1], incluindo registros médicos das atividades do corpo e até ondulações no próprio espaço, criadas pelos eventos astronômicos mais fortes do universo! (Para aprender mais sobre wavelets e processamento de sinais, veja este vídeo, em inglês.) Nos anos 1980, matemáticos, engenheiros e físicos estudavam wavelets simultaneamente. Essa foi uma grande época porque cada campo observava uma parte de um conceito inteiro, que seria extremamente útil em vários outros campos. 

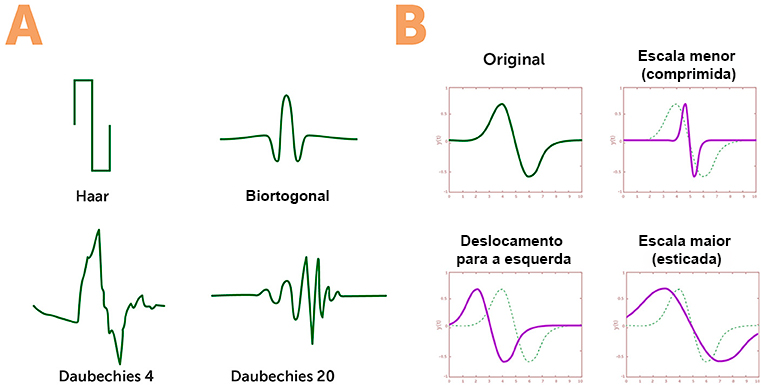
Como o nome sugere, wavelets são pequenas ondas que podem aparecer em vários formatos (Figura 1A). As wavelets são finitas, ou seja, seu valor é não zero só em uma área específica do espaço. Cada wavelets pode ser esticada ou comprimida para ficar mais estreita ou mais larga e também ser deslocada para a esquerda ou para a direita ao longo do eixo x (Figura 1B), a fim de corresponder ao sinal analisado. Você pode pensar nas wavelets como tijolos com os quais podemos reconstruir e analisar sinais e imagens.

Quando queremos analisar um sinal ou imagem, podemos descobrir quais wavelets são mais semelhantes a seus padrões (Figura 2). É importante ressaltar que podemos ajustar a escala para “aumentar” e ver os menores detalhes do sinal (comprimir uma wavelet) ou para “diminuir” e obter uma visão mais ampla dele (esticar a wavelet). Então, aplicando alguns recursos matemáticos, podemos usar wavelets tanto para obter certas informações do sinal ou da imagem, como se eles contivessem a forma ou padrão específico que estamos procurando, quanto para comprimir esse sinal – isto é, salvar a imagem usando apenas uma pequena parte do espaço da memória original, que ainda nos fornece informações suficientes para nosso propósito. 

Wavelets como ferramentas para processamento de imagens

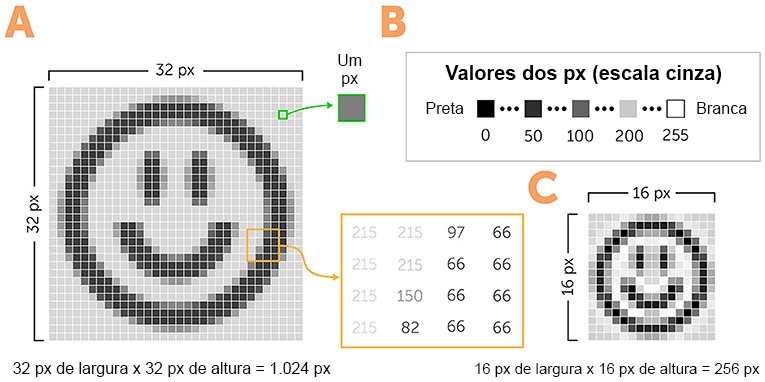
Como você já deve saber, as imagens são representadas nos computadores como conjuntos de números (Figura 3A). Numa imagem de tons de cinza, a cor de cada pixel é representada por um número, muitas vezes na faixa de 0–255 (Figura 3B). O número 0 representa a cor preta e o 255 representa a branca. Todos os números intermediários são vários tons de cinza (se as imagens forem coloridas, usaremos três números para representar os três componentes da cor: vermelho, verde e azul). Os computadores representam todas as informações usando apenas dois estados: “0” e “1”. Cada unidade “0” e “1” é chamada de bit e cada bit pode representar os dois estados.

Quando combinamos dois bits, uma vez que cada um deles pode representar independentemente dois estados, os dois juntos podem representar 2² = 4 estados. Se quisermos representar 256 números (de 0 a 255), precisaremos de um sistema de 8 bits (2⁸ = 256). Uma imagem retangular típica é formada por 512 linhas, cada uma com 512 pixels, portanto 512 x 512 = 262.144 pixels no total. Cada pixel é representado por 8 bites, desse modo, precisaremos de 262,114 x 8 = 2.097.152 bits, ou unidades de informação, para representar apenas uma imagem típica em tons cinza (para imagens coloridas, precisaríamos de três vezes mais!). 

Temos aí uma quantidade enorme de informações, especialmente no caso dos filmes, onde há 25 imagens por segundo, cada uma representada por milhões de bits. Precisamos frequentemente encontrar maneiras de diminuir o tamanho da memória do computador necessária para armazenar imagens, sem perder informações importantes. Podemos, por exemplo, tentar compactar a imagem e reduzir o número de pixels armazenados na memória.

Uma maneira simples de fazer isso é pegar cada dois pixels vizinhos em uma imagem, calcular o número médio de suas cores e salvar apenas um pixel com esse número médio de cores (Figura 3C). Assim, reduzimos o número de pixels de uma imagem para um fator de dois horizontalmente (para pixels vizinhos em cada linha) e para um fator de dois verticalmente (para pixels vizinhos em cada coluna). Podemos repetir esse processo muitas vezes e produzir uma imagem muito pequena. 

Quando fazemos essa média, perdemos informações importantes que estavam contidas na imagem original – informações que tornariam a imagem reconstruída mais borrada. Se não quisermos perder essa informação, teremos de reconstruir a imagem original a partir da imagem média: salvamos as diferenças entre os pixels originais cuja média calculamos, pois é possível encontrar os números originais a partir da média e da diferença de dois números. Acontece que podemos representar essas médias e diferenças usando wavelets!

Se pegarmos as médias e diferenças só entre dois vizinhos próximos, obteremos uma wavelet em forma de escada (onda de Haar na Figura 1A). Muitas vezes, queremos combinar grupos maiores de pixels vizinhos, o que significa que cada pixel calculado conterá mais informações. Ao fazer isso, conseguimos outras wavelets mais suaves (wavelets Daubechies 20 na Figura 1A). 

As wavelets podem nos mostrar as partes mais importantes da nossa imagem, que serão áreas da imagem onde “alguma coisa está acontecendo”, como limites. As wavelets podem nos dar informações sobre tendências gerais nos valores dos pixels de nossa imagem, e sobre detalhes horizontais, verticais e horizontais ou mudanças acentuadas de cor. As wavelets analisam melhor mudanças acentuadas nas imagens (e outros sinais) do que outros métodos comuns de análise de sinais. 

As wavelets permitem identificar e salvar apenas características importantes da imagem, onde há grandes alterações, e descartar informações sobre áreas uniformes. As informações que salvamos sobre os traços importantes são suficientes para nos permitir reconstruir uma versão bastante precisa da imagem original. Salvar apenas 10% ou até 3% dos dados originais muitas vezes basta para obter uma versão muito boa da imagem original (veja este vídeo, em inglês, e verifique se consegue notar as diferenças entre as várias compressões). 

Desenvolvi wavelets que são particularmente úteis para a análise de imagens. Embora a maioria dos cientistas trabalhasse com wavelets conhecidas e tentasse alterá-las a fim de torná-las úteis para análise de imagens, eu me concentrei primeiro na tarefa da análise de imagens disponíveis e perguntei: quais propriedades as wavelets devem ter para cumprir essa tarefa?

Baseados nessas propriedades, meus colegas e eu elaboramos uma família completamente nova de wavelets [2]. Em seguida, mostramos como elas podem ser usadas para a compressão e o processamento da imagem [3]. Nossa sugestão acabou sendo muito útil e foi aplicada em um método chamado padrão de compressão de imagem JPEG2000 [4, 5]. O JPEG2000 é amplamente usado na compressão de imagens de alta resolução, e tem muitas aplicações na Internet e para filmes digitais. 

Wavelets em lugares interessantes

As wavelets são uma poderosa ferramenta para analisar sinais e imagens. Em princípio, podem ser utilizadas em qualquer situação que exija análise de sinais, inclusive nas áreas de astronomia (para a seleção automática das imagens de objetos astronômicos mais nítidas [6]), perícia forense (para detectar manipulações de arquivos digitais de áudio, imagens e vídeos [7]) e medicina (para detectar doenças cardíacas que causam suprimento irregular de sangue para o coração [8]). Com o tempo, à medida que instalamos cada vez mais sensores em nossos ambientes e recolhemos uma quantidade cada vez maior de dados armazenáveis, espero que as wavelets tenham um papel ainda maior em muitas aplicações. 

No momento, meus colegas e eu estamos testando o uso de wavelets em aplicações interessantes e, talvez, bastante surpreendentes. Em um dos meus projetos, por exemplo, trabalho com historiadores da arte. Recorremos às wavelets para analisar pinturas e entender sua história. Especificamente, estamos tentando obter a melhor visualização possível das camadas ocultas, chamadas pinturas de base, que estão embaixo das pinturas visíveis (Figura 4A). Depois de identificar uma pintura de base usando raios X, usamos wavelets para “expor” os detalhes dessa pintura e reconstruí-la com a maior precisão possível. Também podemos usar wavelets para outras aplicações na arte, como estudar e remover (ou gerar) fissuras em imagens digitais de pinturas (Figura 4B) ou rejuvenescer cores envelhecidas. 

Finalizando, gostaria de compartilhar com vocês uma lição importante que aprendi trabalhando com problemas matemáticos. A fim de resolver um problema matemático, você deve abordá-lo repetidamente, por vários “lados”. Isso lembra os esportes, onde temos que trabalhar duro e fazer muito esforço para melhorar – mas o fato de algo ser difícil não significa que seja impossível. Portanto, continue tentando e usando a criatividade para encontrar maneiras novas e bonitas de entender as coisas ao seu redor, procurando sempre compartilhar suas ideias com outras pessoas. 

Glossário

Wavelets ou ondaletas: Funções matemáticas usadas no processamento de sinais e imagens. A palavra “wavelet” significa “pequena onda”. A palavra “ondaleta” também pode ser usada em alguns casos.

Comprimir (dados): Salvar só a parte necessária dos dados. 

Pixel: A menor unidade (círculo pequeno) nas imagens digitais. 

Processamento de imagem: Operação matemática em imagens digitais para extrair delas informações úteis. 

JPEG2000: Método de compressão de imagem baseado em wavelets de Daubechies, muito usado em filmes digitais e na internet.

Conflito de interesses

O autor declara que a pesquisa foi realizada sem nenhuma relação financeira ou comercial capaz de gerar um conflito de interesses.

Agradecimentos

Agradeço a Or Raphael por conduzir a entrevista que serviu de base para este artigo e pela coautoria dele, e a Alex Berstein por fornecer as figuras.

Materiais adicionais

[1] Compression Applet – Using Wavelets to Compress Files (Duke University).

[2] Using Math to Understand Art. Ingrid Daubechies. TEDxDuke.

[3] Mathemalchemy – A Unique and Collaborative Art Exhibit Exploring the Beauty of Mathematics.[4] How Wavelets Let Researchers Transform and Understand Data.

Referências

[1] Daubechies, I. 1992. “Ten lectures on wavelets”, em CBMS-NSF Regional Conferences Series in Applied Mathematics, p. vii (Filadélfia, PA: SIAM).

[2] Cohen, A., Daubechies, I. e Feauveau, J. C. 1992. “Biorthogonal bases of compactly supported wavelets.” Commun. Pure Appl. Math. 45:485 –-560.

[3] Antonini, M., Barlaud, M., Mathieu, P. e Daubechies, I. 1992. “Image coding using wavelet transform.” IEEE Trans. Image Process. 1:205–20.

[4] Usevitch, B. E. 2001. “A tutorial on modern lossy wavelet image compression: foundations of JPEG2000.” IEEE Sign. Process. Mag. 18:22–35. DOI: 10.1109/79.952803.

[5] Unser, M. e Blu, T. 2003. “Mathematical properties of the JPEG2000 wavelet filters.” IEEE Trans. Image Process. 12:1080–90. DOI: 

10.1109/TIP.2003.812329.

[6] Kautsky, J., Flusser, J., Zitova, B. e Simberova, S. 2002. “A new wavelet-based measure of image focus.” Pat. Recogn. Lett. 23:1785–94. DOI: 10.1016/S0167-8655(02)00152-6.

[7] Farid, H. e Lyu, S. 2003. “Higher-order wavelet statistics and their application to digital forensics”, em 2003 Conference on Computer Vision and Pattern Recognition Workshop, vol. 8, p. 94 (Madison, WI: IEEE).

[8] Akay, M. 1997. “Wavelet applications in medicine.” IEEE Spectr. 34:50–6.

Citação

Daubechies, I. (2023). “Wavelets mathematical tools for image analysis.” Front. Young Minds. 11:1200611. DOI: 10.3389/frym.2023.1200611.

Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.