Por que precisamos da matemática na medicina?
Autores
Andrew Dawkins, Catrin S. Rutland, James Cockcroft, Mariam Saigar
Jovens revisores

Resumo
Se você planeja tornar-se médico, inventar tecnologias médicas ou apenas entender os tratamentos a que se submete como paciente, saber a matemática por trás da medicina é essencial. Este artigo investiga como descobrimos se alguém está com coronavírus ou uma doença cardíaca, como calculamos quantas pessoas serão afetadas por enfermidades e como a matemática é usada para tratar pacientes ou impedir a disseminação de moléstias. Embora as pessoas em geral saibam que ciências como a biologia e a química são importantes para trabalhos na área médica, muitas ignoram que a matemática também é vital. Este artigo examina algumas das funções da matemática na medicina e na medicina veterinária. Se você quer ser médico, enfermeiro, cientista médico, exercer alguma profissão ligada a pessoas ou animais ou só deseja estar bem-informado como paciente, o conhecimento da matemática é importantíssimo!
Matemática para estudar a distribuição e a disseminação de doenças
Os epidemiologistas são profissionais médicos que praticam a epidemiologia, o estudo da distribuição, disseminação e prevenção de doenças ou distúrbios como coronavírus, poliomielite, asma, problemas cardíacos e câncer.
Para saber até que ponto uma doença infecciosa é grave, os epidemiologistas precisam conhecer o nível de infecção presente. A taxa de incidência é o número dos novos casos da doença numa população em certo período de tempo (anual, mensal, semanal ou diário). Além do número de novos casos, é necessário saber quanto a doença já se espalhou. A prevalência mostra a proporção de uma população que tem a doença em determinada época, para que possamos ajudar as pessoas certas nas áreas certas. Por exemplo, se 500 pessoas numa cidade de 1.000 (50%) têm coronavírus, isso é bem mais sério do que se houvesse 500 casos numa cidade de 20.000 habitantes (2,5%), embora o número de infectados seja o mesmo.
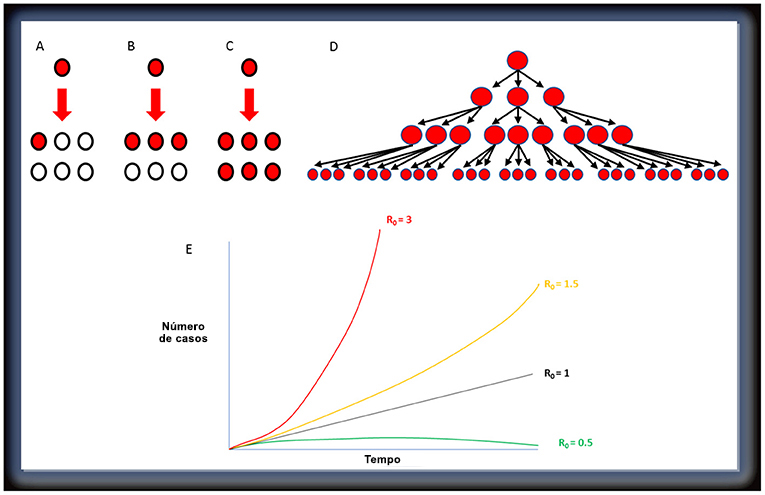
Você talvez já tenha ouvido falar em um número chamado R0 (R zero) recentemente. Ele é chamado também de número básico de reprodução da infecção e significa o número médio de casos novos provocados por um caso existente que chega em uma população completamente suscetível (Figuras 1A – C). O R0 permite que os epidemiologistas entendam como uma infecção passa de uma pessoa a outra.
Um R0 inferior a 1 significa que uma pessoa infectada infectará, em média, menos de uma pessoa, ao passo que se o R0 for maior do que 1, a infecção se espalhará mais rapidamente. Um R0 de 3 talvez não pareça tão ruim assim, mas, se 1 pessoa infectada infectar outras 3, que por sua vez infectarão 3, isso logo resultará em 27 pessoas infectadas (Figura 1D). A isso se dá o nome de crescimento exponencial e os números de novos casos aumentarão cada vez mais rapidamente, a menos que se reduza o R0 e se impeça a disseminação da doença (Figura 1E).
Você poderá ler mais sobre esse assunto em Disease Detectives: Using Mathematics to Forecast the Spread of Infectious Diseases [Detetives de doenças: o uso da matemática para prever a disseminação de moléstias infecciosas] [1]. O R0 é afetado pela densidade populacional, pela quantidade de pessoas vulneráveis, pela frequência de contatos entre elas e pela transmissibilidade do agente infeccioso.
A matemática no diagnóstico de condições médicas e doenças
Antes de poder calcular R0, precisamos identificar quantas pessoas estão realmente infectadas por um agente infeccioso. A matemática ajuda a garantir que problemas médicos sejam corretamente identificados e diagnosticados. Os testes de doenças cardíacas ou diabetes são chamados de testes diagnósticos e envolvem o cálculo das quantidades de certas substâncias em amostras de sangue ou outras. O exame de amostras fornece um amplo leque de resultados:
- Verdadeiros positivos: resultados positivos que detectam a presença da doença
- Falsos positivos: resultados positivos mesmo quando a doença não está presente
- Verdadeiros negativos: resultados negativos sem a presença da doença
- Falsos negativos: resultados negativos embora a doença esteja presente
Acurácia de diagnóstico é a medida da eficiência do teste diagnóstico para revelar a diferença entre pacientes saudáveis e doentes. É calculada usando-se esta equação:
A acurácia de diagnóstico não revela o quadro completo, de modo que avaliações de sensibilidade e especificidade também são necessárias [2]. A sensibilidade de um teste diagnóstico é sua capacidade de identificar corretamente verdadeiros positivos; a especificidade de um diagnóstico é sua capacidade de identificar corretamente verdadeiros negativos:
Um resultado negativo em um teste com 100% de sensibilidade significa que o paciente não tem, em definitivo, a doença. No entanto, um resultado positivo em um teste de alta sensibilidade não significa que a doença esteja presente. É aí que a especificidade se torna útil. Um resultado positivo em um teste de alta especificidade confirma a doença. Idealmente, testes diagnósticos são ao mesmo tempo altamente sensíveis e específicos, embora às vezes não possamos ter os dois.
Além de exato, um teste diagnóstico deve apresentar alta precisão. A precisão é a capacidade de um teste de produzir resultados confiáveis sempre que for usado. Ela é calculada usando-se a seguinte equação:
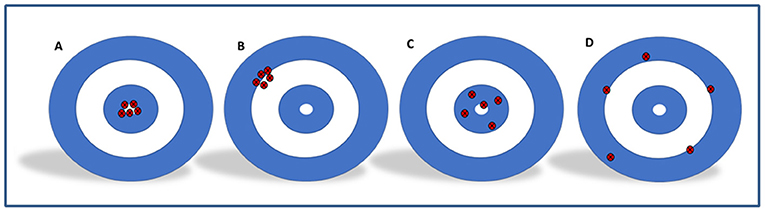
Esses conceitos são ilustrados usando-se a prática do arco e flecha como exemplo na Figura 2.
A matemática nas doenças cardíacas
Muitas pessoas são monitoradas por um eletrocardiógrafo (ECG) quando têm uma doença ou uma suspeita de doença cardíaca, mas também quando não se sentem bem por qualquer outro motivo. O ECG mede o tamanho e o ritmo dos sinais elétricos no coração por intermédio de eletrodos colocados no peito, braços e pernas do paciente. Essas informações são em seguida mapeadas no eletrocardiograma (Figura 3ª).
O eletrocardiograma possui uma forma especial, com letras marcando os picos e depressões. A onda P é a contração dos átrios (câmaras na parte superior do coração). (Procure mais informações em Mending a Broken Heart – The Genetics of Heart Disease [Remendando um coração partido – a genética da doença cardíaca], Front Young Minds [3].) Nos pontos QRS vê-se a contração dos ventrículos (parte inferior do coração). A onda R é grande porque os ventrículos são a parte maior do coração. A parte final do ciclo é mostrada pela onda T. As várias partes do eletrocardiograma podem ser analisadas para se descobrir se o coração está funcionando bem.
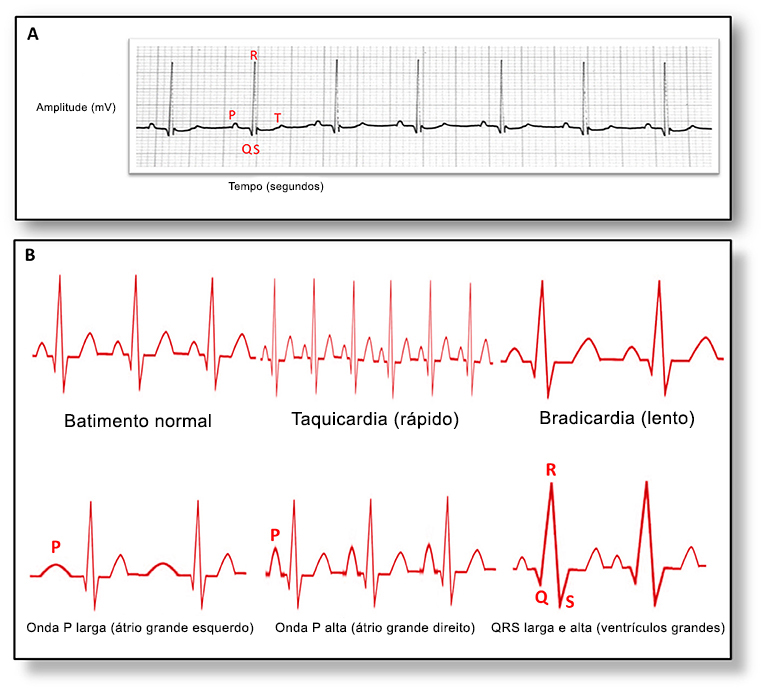
(A) As letras representam diferentes fases do ciclo de batimentos. A fim de determinar a frequência cardíaca, a distância entre duas ondas R é medida e convertida em tempo. Por exemplo, se a distância entre duas ondas R é de 12,5 mm e cada mm representa 0,04 s; portanto, 12,5 x 0,04 = 0,5 s entre os batimentos. Como a frequência de batimentos é calculada como pulsações por minuto, 60 s/0,5 = 120 pulsações por minuto. (B) O ECG pode ser usado para diagnosticar diversas doenças do coração com base na forma e no espaçamento das ondas.
Caso a forma e o tempo dessas ondas sejam anormais, o coração pode estar funcionando mal (Figura 3B). O espaço entre as ondas R mostra a frequência cardíaca. Batimentos rápidos são chamados de taquicardia; batimentos baixos, de bradicardia. Ambas as condições podem ser perigosas. Uma onda P muito larga às vezes significa que o átrio esquerdo aumentou de tamanho; uma onda P mais alta pode significar que o átrio direito está maior. Anormalidades na onda T podem ter várias causas, são bastante comuns e nem sempre geram problemas sérios. Se o complexo QRS for largo e alto, os ventrículos provavelmente estão aumentados. Isso se chama cardiomegalia e pode ser sinal de insuficiência cardíaca, infecção nos tecidos do coração ou pressão alta.
Outros usos da matemática na medicina
Os cardiologistas e médicos de outras especialidades podem também querer examinar a estrutura do coração, dos vasos sanguíneos ou outros órgãos. Há diversos métodos usados para “ver” dentro do corpo, como os raios-X, a tomografia computadorizada (TC), o ultrassom e a ressonância magnética (RM)[4]. Todas essas técnicas de imagem exigem a matemática: as avaliações devem ser exatas, pois não há lugar para o erro em medicina.
Depois que uma condição médica é diagnosticada, os pacientes precisam ser monitorados e receber medicação adequada. Calcular as doses dos remédios exige recursos matemáticos como a soma, a fração e a equação algébrica. Esses cálculos são extremamente importantes porque uma dose capaz de ajudar um adulto pode prejudicar uma criança, enquanto uma dose para criança talvez não seja suficiente para um adulto. Muitas doses são dadas por quilo ou peso corporal.
Quando um paciente precisa de cirurgia, os profissionais médicos aferem sua pressão, calculam os níveis de oxigênio, monitoram a temperatura do corpo e a frequência respiratória, e administram doses corretas de anestesia e fluidos. (Para saber mais sobre anestesia, ver What Is Anesthesia? [O que é anestesia?] [5].) Elaborando e utilizando gráficos e equações, os profissionais médicos conseguem determinar se o paciente está melhorando ou piorando e do que ele precisa durante o tratamento.
Conclusões
Muitas são as maneiras pelas quais a matemática se mostra vital na medicina humana e veterinária. Os profissionais médicos calculam o risco da disseminação de uma doença, a quantidade de remédios a ministrar, o ritmo em que o coração bate e a condição de melhora ou piora de um paciente. Da próxima fez que você estudar matemática, pense em quanto ela pode ser útil a médicos, enfermeiras, veterinários, cientistas e outros profissionais que trabalham para nos tornar mais saudáveis. Se estiver pensando em seguir uma dessas carreiras no futuro, não se esqueça de que suas aulas de matemática são tão importantes quanto as de ciências!
Glossário
Epidemiologia: Estudo da distribuição e das causas/fatores de risco da doença ou de outras condições de saúde nas populações.
Taxa de incidência: A taxa de novos casos de uma doença em um grupo conhecido da população em um dado período de tempo.
Prevalência: A proporção de uma população que tem a doença em um dado período.
R0: O número/taxa básico de reprodução que mostra o grau de contágio de uma doença infecciosa.
Teste diagnóstico: Um teste médico usado para diagnosticar uma doença ou condição de saúde.
Acurácia de diagnóstico: A capacidade de um teste de determinar a diferença entre pacientes saudáveis e doentes.
Eletrocardiógrafo: Equipamento para medir a atividade elétrica no coração, o que ajuda a descobrir se esse órgão está funcionando corretamente.
Agradecimentos
Parte deste trabalho foi possível graças à bolsa escolar INSPIRE financiada pela Wellcome Trust, Academy of Medical Sciences, concedida aos drs. C. S. Rutland, V. James, K. Braithwaite, K. Cobb e profs. N. Mongan e G. England para realizarem pesquisas e engajamento público. Somos gratos ao prof. Malcolm Cobb por nos fornecer o ECG usado na Figura 3. Somos gratos também à Linnean Society e ao National Literacy Trust por apoiarem Catrin como embaixadora de temas científicos junto aos jovens. Agradecemos ainda à British Science Association e à Universidade de Nottingham por concederem um BSA Media Fellowship a Catrin.
Referências
[1] Brooks, H., Kanjanasaratool, U., Kureh, Y. e Porter, M. 2021. “Disease detectives: using mathematics to forecast the spread of infectious diseases.” Front. Young Minds. 9:577741. DOI: 10.3389/frym.2020.577741.
[2] Sitch, A. J., Dekkers, O. M., Scholefield, B. R. e Takwoingi, Y. 2021. “Introduction to diagnostic test accuracy studies.” Eur. J. Endocrinol. 184:E5–9. DOI: 10.1530/EJE-20-1239.
[3] Clark, N., Alibhai, A. e Rutland, C. S. 2018. “Mending a broken heart – the genetics of heart disease.” Front Young Minds 9:19. DOI: 10.3389/frym.2018.00019.
[4] Keane, M., Paul, E., Sturrock, C. J., Rauch, C. e Rutland, C. S. 2017. “Computed tomography in veterinary medicine: currently published and tomorrow’s vision”, em Computed Tomography – Advanced Applications, org. A. M. Halefoglu (Londres: IntechOpen), pp. 271-89
[5] Lendner, J. 2021. “Wha tis anestesia?” Front. Young Minds 9:524571. DOI: 10.3389/frym.2021524571
Citação
Cockcroft, J., Saigar, M., Dawkins, A. e Rutland, C. (2021). “Why Do We Need Maths in Medicine?” Front. Young Minds. 9:678802. DOI: 10.3389/frym.2021.678802.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Agradecemos a Ricardo Mattos Ferreira, da Faculdade de Medicina da Unesp em Botucatu, e Claudia Pio Ferreira, do Instituto de Biociências da Unesp em Botucatu, pela leitura atenta.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br