Teoria dos jogos e cooperação: por que pensar primeiro nos outros beneficia a todos
Autores
Jovens revisores
Katherine Johnson Scholar Sisters

Resumo
Leo Durocher, famoso jogador de beisebol dos anos 1930, disse certa vez: “Bons rapazes acabam em último lugar”. Isso pode ser verdade no beisebol, mas não na vida de um modo geral. Neste artigo, usamos ideias de um ramo da matemática conhecido como “teoria dos jogos” para estudar uma situação chamada “Dilema dos Prisioneiros” (DP), que lança luz sobre o motivo de as pessoas muitas vezes não conseguirem trabalhar bem juntas. A teoria dos jogos mostra que pessoas gentis e confiáveis gozam de uma vantagem estratégica, pois podem “mudar o jogo” para escapar ao DP e criar uma situação melhor para os outros e para si mesmas. Assim, na verdade “bons rapazes acabam em primeiro lugar”.
Introdução: jogos, jogos por todo lado
“Nenhum homem é uma ilha, nenhum basta a si mesmo.” (John Donne, poeta inglês do século 17)
Quando as pessoas falam em “jogos”, geralmente pensam em diversões como damas e Banco Imobiliário ou esportes como futebol e basquetebol. Entretanto, no ramo da matemática conhecido como “teoria dos jogos”, eles têm um sentido bem mais amplo.
Definição de jogo
Uma situação é um “jogo” quando: (i) mais de uma pessoa toma uma decisão e (ii) as decisões das pessoas afetam a todas.
Quase tudo que fazemos na vida é um jogo no sentido da teoria dos jogos. Jogamos em casa, na escola, aonde quer que vamos, em praticamente tudo. Não acredita? Pense no começo de seu dia, quando acordou. A rapidez com que você saltou da cama afetou seus pais e a hora em que eles o acordaram afetou você: então, foi um jogo! Pense também no que aconteceu depois, ao longo do dia. Do banheiro à mesa do café da manhã, na sala de aula e no pátio do recreio, você faz escolhas que afetam os outros e a você igualmente. Você joga! Conhecer a teoria dos jogos pode ajudá-lo a enriquecer sua experiência nessas situações – não apenas a “vencer”, mas a melhorar seus relacionamentos para levar uma vida mais feliz.
A teoria dos jogos é usada para estudar como as pessoas provavelmente irão se comportar em situações estratégicas, com aplicações na economia, na ciência política, nos negócios, no direito, no empreendedorismo e na ciência militar, para só citar algumas. Assim como a física descreve como os planetas giram em torno do Sol, a teoria dos jogos procura descrever de que modo as pessoas tomam decisões nos jogos. A matemática é útil na teoria dos jogos como ferramenta para analisar as motivações dos jogadores e predizer resultados. Às vezes, como no exemplo a seguir, as predições feitas pela teoria dos jogos podem ser bastante inesperadas.
Exemplo: comer fora com amigos
Oito amigos decidiram ir comer numa lanchonete. Vão dividir a conta igualmente. Há dois itens no cardápio: (i) um hambúrguer comum, que custa $4, e (ii) um hambúrguer especial, que custa $8. Cada amigo conclui que comer um hambúrguer comum vale $5 e que comer um especial vale $6. Note que o hambúrguer comum vale mais do que custa ($ > $4), enquanto o especial vale menos do que custa ($6 < $8). O hambúrguer especial é obviamente um mau negócio: terão de pagar $8 por algo que vale apenas $6 para eles. Entretanto, a teoria dos jogos prevê que, quando comerem juntos, os oito amigos vão pagar por hambúrgueres especiais. Por quê?
Para entender esse desfecho inesperado, convém pensar no jogo a partir de um ponto de vista matemático. Seja D o número de amigos que pedem hambúrgueres especiais e R o dos que pedem hambúrgueres comuns. (D e R são inteiros de 0 a 8, com R + D = 8, pois há oito amigos no total.) Como os hambúrgueres especiais custam $8 e os comuns custam $4, a conta total será 8D + 4R. Como R = 8 – D, podemos reescrever isso como 8D + 4 (8 – D). Multiplicando, obtemos 8D + 32 – 4D, o que pode ser simplificado assim:
Conta total = 32 + 4D
A conta de cada amigo é 1/8 da conta total. Como a conta total é 32 + 4D, cada amigo paga 32/8 + 4D/8, o que pode ser simplificado assim:
Conta individual = 4 + D/2
Quando alguém troca seu pedido de “comum” para “especial”, obtém um dólar extra de valor do hambúrguer (agora ele vale $6 para ele, em vez de $5). No entanto, paga apenas 50 centavos a mais, pois o custo adicional de $4 para o especial é dividido oito vezes. Cada pessoa, então, se sente motivada a pedir um hambúrguer especial ainda que, se todos fizerem isso, acabe pagando $8 por algo que para ela vale apenas $6. (Que aconteceria se uma pessoa do grupo decidisse pedir um hambúrguer comum? A conta total cairia de $64 para $60, fazendo com que a conta de cada um caísse de $8 para $7,50. Assim, a pessoa que pedisse o hambúrguer comum teria de pagar $7,50 por algo que para ela vale apenas $5: pior do que pagar $8 por algo que para ela vale $6.)
Isso parece estranho, mas, de fato, é um exemplo da situação estratégica mais famosa e estudada na teoria dos jogos – o jogo chamado “Dilema dos Prisioneiros (DP)”.
O Dilema dos Prisioneiros
Albert Tucker, matemático de Princeton e antigo teórico dos jogos1, elaborou a história do DP em 1950 para demonstrar uma inesperada lição da teoria dos jogos: às vezes, fazer o que é melhor para nós individualmente pode prejudicar a todos.
História do DP
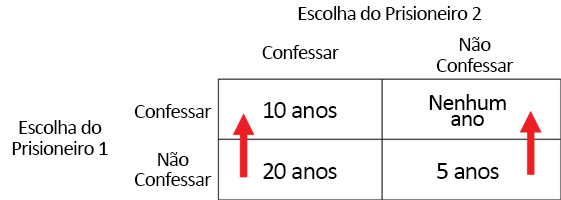
A polícia capturou dois criminosos – “Prisioneiro 1 (P1)” e “Prisioneiro 2 (P2)” – por acusações que poderiam valer-lhes até 5 anos de prisão. Mas a polícia tinha fortes suspeitas de que eles haviam cometido também um crime pior, roubo à mão armada, que acarretaria uma pena de 20 anos. O policial encarregado do interrogatório coloca-os em celas separadas e diz a cada um: “Já é hora de vocês confessarem o roubo. O tempo de detenção dependerá de quem confessar. Se só você confessar, ficará livre hoje. Mas permanecerá 5 anos atrás das grades se nenhum dos dois confessar, 10 anos se ambos confessarem ou 20 anos se você for o único a não confessar”. Que farão os prisioneiros?
A Figura 1 mostra quanto tempo P1 passará na cadeia, dependendo de quem se disponha a confessar. Observe que, não importa a atitude de P2, P1 levará vantagem se confessar. (Se P2 confessar, isso fará com que P1 passe 10 anos e não 20 na cadeia; se P2 não confessar, isso fará com que P1 saia livre em vez de permanecer 5 anos preso. De qualquer modo, P1 tem uma motivação pessoal para confessar.) Essa lógica, é claro, se aplica também a P2. Assim, a teoria dos jogos prevê que ambos os prisioneiros confessarão e ambos ficarão 10 anos presos – um resultado do tipo “perder-ou-perder”, já que os dois poderiam passar apenas 5 anos na cadeia caso ambos ficassem calados.
O DP na vida real
Você provavelmente nunca será interrogado pela polícia, mas muitas situações que enfrentamos na vida são, em essência, as mesmas que o DP, do ponto de vista da teoria dos jogos. Para deixar isso o mais claro possível, convém definir melhor o que entendo por “Dilema dos Prisioneiros”. Assim, poderemos saber com mais facilidade quando uma situação do mundo real é um DP, mesmo sem prisioneiros envolvidos. Para isso, preciso antes definir outro conceito importante da teoria dos jogos, a “estratégia dominante”.
Definição de estratégia dominante
Uma “estratégia dominante” é aquela que oferece ao jogador o melhor retorno possível, não importam as ações que os outros empreendam.
Definição do Dilema dos Prisioneiros
Um jogo é um “Dilema dos Prisioneiros” sempre que (i) todos os jogadores tenham uma estratégia dominante e (ii) os jogadores se saiam melhor caso todos prefiram não aplicar suas estratégias dominantes.
Essa definição do PD não diz nada sobre o número de jogadores no jogo. Na história clássica, só há dois prisioneiros, mas isso não é importante. O mesmo jogo básico poderia ser jogado com qualquer outro número de prisioneiros. Por exemplo, o jogo “Comer Fora com Amigos” que examinamos mais acima é um DP com oito jogadores; a estratégia dominante é “peça um hambúrguer especial” (em vez de “confesse”); e o mau resultado coletivo é “cada qual paga mais por seu sanduíche” (em vez de “cada qual passa mais tempo na cadeia”). Aqui vão outros dois exemplos de DP, com muitos jogadores, que encontramos no cotidiano.
Exemplo: Sujeira
Todo fim de semana, amantes de piquenique num parque local precisam decidir o que farão de seu lixo. Individualmente falando, cada pessoa preferiria deixar seu lixo no chão – é incômodo levá-lo até o cesto –, mas, se todos fizerem isso, o parque virará uma bagunça. Nesse DP jogado por amantes de piquenique, a estratégia dominante de cada um é deixar o lixo por ali mesmo, provocando um desfecho coletivamente mau, que é um parque sujo.
Exemplo: Resistir ao valentão
Em sua classe, há um valentão que agride todo mundo. Quando ele está agredindo alguém, você sai em defesa da vítima ou fica de lado, sem fazer nada? Individualmente falando, você e todos os outros garotos da classe preferem não enfrentar o valentão – ele poderá agredi-los também –, mas, se ninguém fizer nada, o valentão não vai parar nunca. Nesse DP jogado por garotos, a estratégia dominante de cada um é não enfrentar o valentão, o que trará um mau resultado: as agressões continuarão.
Como escapar do DP: o poder de ajudar os outros
“Faça aos outros o que deseja que lhe façam”. (Regra de Ouro)
No DP, cada qual obtém um mau resultado quando exige o que é melhor para si individualmente em vez de fazer um sacrifício pessoal para ajudar os outros. Uma maneira de escapar do DP é, portanto, alterar as motivações dos jogadores para que eles desejem ajudar os outros. Por exemplo, no caso da sujeira no parque, a associação de moradores locais pode colocar cartazes instando os amantes de piquenique: “Seja um bom vizinho. Jogue seu lixo no cesto”. Enfatizando que “bons vizinhos” jogam seu lixo no cesto, esses cartazes certamente induzirão as pessoas a terem mais asseio para se sentirem “bons vizinhos” – e não serem consideradas “maus vizinhos”. Se esse sentimento for forte o bastante para convencer todos a descartarem corretamente seu lixo, eles levarão vantagem porque o parque ficará limpo e se sentirão melhor com respeito a si próprios e aos vizinhos por agirem bem.
Como escapar do DP: o poder das promessas
“Você coça minhas costas e eu coço as suas.” (Velho ditado, oriundo possivelmente de marinheiros ingleses do século 17)
No século 17, marinheiros ingleses apanhados bebendo em serviço enfrentavam severa punição. Eram amarrados no mastro do navio e surrados com um chicote (conhecido como “gato de nove rabos”) por outro membro da tripulação. Para evitar ferimentos sérios, os marinheiros combinavam entre si bater de leve (apenas “coçando” as costas uns dos outros). Se todos aceitassem o acordo, cada qual teria certeza de receber chicotadas leves quando chegasse sua vez de ser punido.
“Você coça minhas costas e eu coço as suas” é um exemplo de promessa – o compromisso de fazermos algo para ajudar outra pessoa se esta primeiro fizer algo para nos ajudar. Uma promessa pode também ajudar jogadores a escapar do DP.
A Promessa do Prisioneiro
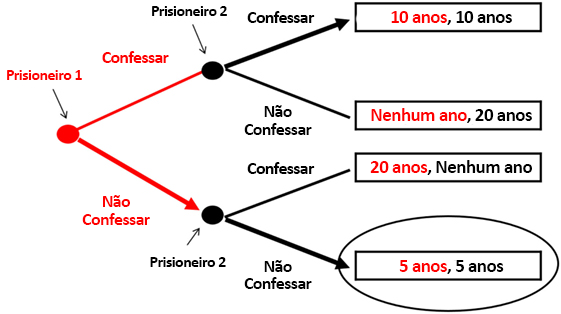
Se você não confessar, prometo que também não confessarei; mas, se você confessar, eu confessarei também.
Suponha que P2 faça essa promessa e P1 acredite nela. A escolha de P1 é, então, entre 10 anos de cadeia (se ambos confessarem) ou 5 (se nenhum confessar) e ele resolve não confessar. DP resolvido! (Ver Figura 2.) Mas e se P1 não acreditar em P2? Se P1 pressentir que P2 quebrará sua promessa, P1 confessará e os dois ficarão na cadeia por 10 anos. O dilema continua!
Como saber se os outros acreditarão em sua promessa? Com maior probabilidade acreditarão se você for uma pessoa honesta e honrada. Se acharem que “sua palavra não volta atrás” e que você se preocupa com sua reputação, eles lhe darão crédito e terão certeza de que fará o que prometeu. Poderá então usar plenamente o poder das promessas para escapar do DP em situações pessoais, beneficiando a você mesmo e aos outros.
Nota
[1] Um aluno de doutorado de Tucker, John Nash, ganhou o Prêmio Nobel de Economia por sua contribuição à teoria dos jogos. O filme laureado com o Oscar, Uma Mente Brilhante, conta a história de Nash, interpretado por Russell Crowe, durante o tempo em que foi aluno de Tucker em Princeton.
Citação
McAdams, D. (2017). “Game theory and cooperation: how putting others first can help everyone.” Front. Young Minds. 5:66. DOI: 10.3389/frym.2017.00066.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br