O zero, um herói esforçado!

Imagine por um minuto como seria sua vida sem esse pequeno círculo que usamos para representar o zero!

Nós hoje tomamos o zero como algo natural, mas é uma invenção relativamente nova. Babilônios e romanos não tinham uma maneira de representá-lo com um símbolo distinto; nem os gregos, que não consideravam o “nada” como um número. Os maias, um povo da América Central, usavam a ideia de zero [1] em seu sistema de calendário, mas, por estarem isolados de outros povos, esse conceito não ultrapassou sua própria civilização. Para encontrar a origem do zero, temos de procurar em outra parte.

Vejamos os algarismos usados na antiga Babilônia, onde existia um sofisticado sistema matemático há mais de 5.000 anos. Esse sistema foi desenvolvido e refinado a partir de outras formas ainda mais antigas de escrever números e fazer cálculos! Sabemos muito sobre o sistema babilônico porque eles escreviam em tabletes de argila que sobreviveram.

Os babilônios eram bons matemáticos e astrônomos que empregavam um complicado sistema de base 60 em vez de nosso sistema de base 10. Na matemática moderna, também usamos a base 60 para certas funções. Por exemplo, o modo como contamos o tempo: 60 segundos num minuto, 60 minutos numa hora. Os babilônios, do mesmo modo que nós, usavam posições (como nossos 10s, 100s, 1.000s de base 10) para representar números. Contudo, usar o sistema de base 60 significa que calcular e determinar as casas era extremamente difícil. Nesse sistema de base 60, as posições se tornam 6s, 60s, 600s, 6.000s. Imagine que está tentando localizar posições sem o símbolo do zero para assinalar o espaço. O pequeno símbolo de zero é muitíssimo útil. Os babilônios por fim começaram a assinalar a coluna vazia com um espaço, mas você bem pode adivinhar como era fácil não perceber um espaço em colunas de números.

Com esse sistema complicado, os babilônios tinham de apelar para o contexto a fim de entender o significado de um número. Um exemplo de contexto: se alguém lhe diz que algo custa oito-cinquenta, você pode presumir que se trata de R$ 8,50 caso esteja pensando em pedir um sorvete, e não R$ 850,00, o que pareceria lógico se estivesse comprando uma passagem de avião.

Os gregos conheciam o zero como conceito, mas não viam nele a mesma utilidade em matemática que os números de 1 a 9. Segundo Aristóteles, não era possível dividir por 0 e obter um resultado significativo; portanto, o sistema grego se baseava em nove números – sem zero.

Os romanos não usavam algarismos para cálculos, por isso não precisavam de um zero para determinar uma casa ou manter uma coluna vazia. O sistema numeral romano era usado para o comércio e não exigia a representação do zero com um símbolo especial. Para fazer contas, recorriam a um ábaco e seus algarismos serviam apenas para escrever os resultados. Isso não significa que não entendessem o nada. Tinham uma palavra para significar “nada”, mas nenhum símbolo.

Superzero!

Por que nos preocupamos com o zero? Ele pode ser usado como marcador de posição, sem valor próprio, ou como número matemático. Por exemplo, quando denominamos um ano como 2019, cada algarismo tem sua própria casa bem definida. Chamamos o zero de marcador de posição porque nos diz que ali não há nenhum 100. Podemos representar nosso sistema, de base 10, mediante colunas, como se vê abaixo:

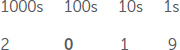
Esse 0 mantém os 1s de cada lado “em suas casas”, de modo que conhecemos seu valor. Se tirarmos esse marcador de posição, não saberemos mais qual é o número.

Mas o zero pode ser mais que um marcador de posição: ele indica também o ponto que divide números positivos e números negativos. Se contarmos retroativamente com números inteiros, chegaremos ao zero; e também chegaremos ao zero se contarmos para a frente com números negativos:

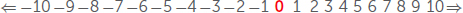
Se você quiser apenas contar e medir, poderá fazer isso sem o zero. Mas, sem zero, a matemática avançada seria impossível: não haveria nem álgebra nem cálculo diferencial. E não teríamos computadores, pois eles usam um sistema binário, de base 2, pelo qual a informação é registrada e lida como uma série de 0s e 1s.

Quem inventou o zero?

Na Idade Média – séculos depois da grande era da matemática grega –, os árabes se revelaram ao mesmo tempo notáveis matemáticos e importantes transmissores do conhecimento antigo, inclusive a matemática. Muhammad ibn Musa al-Khwarizmi foi um famoso matemático, astrônomo e geógrafo persa que contribuiu muito para nossa moderna compreensão da matemática, sobretudo nas áreas de álgebra e trigonometria. Seu nome – Al- Khwarizmi – acabou se transformando em Algorithmi na passagem para o latim. Da forma latinizada, temos o nome algoritmo, que significa a série de regras a serem seguidas quando fazemos cálculos. No início do século 9 d. C., Al-Khwarizmi era astrônomo e bibliotecário-chefe da célebre Casa da Sabedoria em Bagdá, onde ele estudou manuscritos científicos e matemáticos, inclusive os dos antigos gregos e indianos.

Em Al’Khwarizmi sobre a Arte Indiana de Contar, ele descreve um sistema numérico indiano baseado em 10 numerais: 1–9 e 0. Atribui o crédito do zero ao estudioso indiano Brahmabgupta (século 7 d. C.), afirmando que o descobriu quando traduzia suas obras matemáticas. Esse utilíssimo sistema logo foi adotado no mundo árabe. 

O zero faz uma longa viagem até a Europa

Na Idade Média, os europeus ainda faziam negócios usando os algarismos romanos. Entretanto, as rotas de comércio faziam mais que transportar sedas e especiarias do Oriente para o Ocidente – transportavam também conhecimento. Fibonacci, filho de um mercador italiano, sempre viajava a serviço do pai. Na África do Norte, descobriu que comerciantes árabes estavam usando um sistema de contagem baseado em dez números, 1 – 9 + 0. Logo percebeu que esse sistema poderia facilitar a contabilidade e a escrituração na Europa. Em 1202, publicou um livro chamado Liber Abaci (Livro do Ábaco ou Livro do Cálculo) que disseminou a ideia desse novo sistema numérico com o zero “para manter as fileiras”. O livro falava das aplicações práticas do sistema: como converter uma moeda em outra, como calcular lucros e perdas e outros problemas importantes dos negócios [2].

A pesquisa vai à Índia e ao Camboja

Georges Cœdès estava no início da quadra dos vinte anos quando visitou a Coleção do Oriente Próximo no Louvre, o famoso museu de Paris perto do qual morava. Uma inscrição babilônica em exibição o intrigou. Essa experiência precoce incentivou-o a estudar línguas antigas e dedicar a vida à descoberta de velhos mistérios escondidos em inscrições do sudeste da Ásia.

Cœdès elaborou uma teoria curiosa. Achava que os algarismos haviam se originado em civilizações asiáticas que partilhavam uma cultura comum, baseada nas religiões budista e hinduísta. Outros estudiosos da época presumiam que os números deviam ter vindo da Grécia ou da Arábia; Cœdès, porém, sentia que essa crença ignorava o valor dos progressos intelectuais do Oriente. Mas ainda não tinha provas de sua teoria. Então, no curso de seu trabalho, deparou-se com uma inscrição não traduzida, em pedra, que chamou de K-127, oriunda de um antigo templo de Sambor, às margens do Mekong, no Camboja. Ao traduzir o texto, ficou espantado ao perceber que ele continha o esquivo zero que tanto esperava encontrar! (Figuras 1, 2).

A inscrição registra as transações de um mercador e inclui uma data com um zero marcador de posição, representado por um pequeno ponto! Quem entalhou a inscrição teve o cuidado de acrescentar a data: 605 da era Çaka. Converter essa data para nosso próprio calendário não foi difícil. Cœdès sabia que o primeiro rei da era Çaka iniciou seu reinado no ano 78; assim, acrescentando 78 ao 605 da pedra, concluiu que a inscrição fora feita no ano 683 d. C. Cœdès tinha sua prova, que publicou num artigo científico em 1931 [3]. A descoberta revelava que o zero se originara no Oriente porque o encontrado no Camboja fora entalhado antes da obra dos matemáticos árabes. Esse primeiro achado mostrava que nossos algarismos e o zero tinham origem oriental, asiática [4].

Outra reviravolta em nossa teoria dos números

Cerca de quarenta anos antes de Cœdès traduzir a K-127, um manuscrito redigido em casca de salgueiro, chamado Manuscrito Bakhsali, foi descoberto nessa localidade, no atual Paquistão. O texto exibia um antigo zero representado por um pequeno círculo. Sua idade era desconhecida, mas alguns especialistas achavam que devia ser muito antigo. Ao contrário da K-127, esse texto não incluía uma data, de modo que foi difícil determinar quando tinha sido escrito. Além disso, os estudiosos supunham que partes do manuscrito haviam sido redigidas em épocas diferentes.

Hoje, o Bakshali está na Biblioteca Bodleiana da Universidade de Oxford. Em 2017 [5], a biblioteca permitiu que um fragmento da casca fosse removido para datação por radiocarbono. Os resultados indicaram que a parte onde aparece o zero é do século 3 ou 4. Se isso estiver correto, o manuscrito Bakhshali é mais velho que a pedra K-127, mais velho que qualquer inscrição já descoberta onde se vê o zero. Alguns eruditos não estão convencidos. Seu argumento é que a parte removida para teste não contém inscrição nenhuma e que, segundo se pensa, as páginas foram escritas em épocas diferentes. Isso cria um problema. Os cientistas esperam que a Biblioteca Bodleiana faça mais testes com outras partes do manuscrito.

Muitas perguntas subsistem. Até que ponto o método empregado na datação do manuscrito é preciso? Outros zeros, ainda mais velhos, serão descobertos? E por fim: de que modo a ideia do zero passou da Índia para o Camboja e a Indonésia, para depois se espalhar pelo resto do mundo? Só sabemos que o zero usado hoje por nós nasceu no sudeste da Ásia! Talvez historiadores futuros da matemática consigam juntar mais peças desse intrigante quebra-cabeça.

História solucionada?

Mas por que a civilização indiana inventou o zero? Se os gregos achavam que o zero era nada, o nada era muito importante para certas religiões orientais, incluindo o budismo e o hinduísmo. Talvez a religião e a filosofia indianas tenham a chave do mistério. Seja como for, a matemática – e os números – ainda guardam muitos segredos para você explorar.

Glossário

Sistema de base 60 (sexagesimal): Antigo sistema numérico que tem por base o 60. Foi usado pelos antigos sumérios no terceiro milênio a. C. e transmitido aos antigos babilônios, sendo ainda usado hoje em dia para medir o tempo, os ângulos e as coordenadas geográficas.

Sistema de base 10 (decimal): Nosso sistema numérico atual, que tem por base o 10, isto é, 10 algarismos. Usa valor posicional e ponto decimal para separar números inteiros de frações decimais.

Marcador de posição: Número sem valor próprio, usado em decimais e retas numéricas para mostrar o valor de outros números.

Números inteiros: Números não decimais e não fracionários (como 1, 2, 3, etc.).

Sistema de base 2 (binário): Sistema no qual a informação pode ser expressa por combinações dos dígitos 0 e 1.

Idade Média: Período de tempo da história europeia desde a queda do Império Romano do Ocidente (476 d. C.) até a tomada de Constantinopla pelos turcos (1453).

Datação por radiocarbono: Método científico usado para determinar a idade de um objeto com base em um isótopo radiativo do carbono.

Conflito de interesses

Os autores declaram que a pesquisa foi conduzida sem nenhuma relação comercial ou financeira que possa constituir um conflito de interesses.

Referências

[1] Ifrah, G. 2000. The Universal History of Numbers. New York, NY: John Wiley & Sons, Inc.

[2] Walker Publishing Co. 2011. The Man of Numbers: Fibonacci’s Arithmetic Revolution. London: Walker Publishing Co.

[3] Cœdès, G. 1931. “A propos de l’origine des chiffres arabes.” Bull. School Orient. Stud. 6:323–8.

[4] Cœdès, G. 1968. The Indianized States of Southeast Asia. Honolulu, HI: University of Hawaii Press.

[5] Oxford University News. 2017. Earliest Recorded Use of Zero Is Centuries Older Than First Thought. Disponível em: http://www.ox.ac.uk/news/2017-09-14-earliest-recorded-use-zero-centuries-older-first-thought.

Citação

Aczel, M., Aczel, D. e Ville, M. (2019). “Hero from the East: how zero came to the West.” Front. Young Minds. 7:128. DOI: 10.3389/frym.2019.00128.