Um desafio à gravidade? Os truques de mágica dos superfluidos
Autores
Jovens revisores

Resumo
A física é uma das melhores ferramentas de que dispomos para resolver quebra-cabeças em nosso mundo. Esses quebra-cabeças podem ser perguntas sobre fenômenos comuns que você vê ao seu redor, como o vento soprando nos galhos de uma árvore; ou então sobre outros eventos bastante raros e misteriosos que só acontecem em condições específicas. Minha jornada com a física me pôs em contato com um fenômeno dos mais intrigantes, em que um fluido normal é resfriado e de repente muda suas propriedades fundamentais para se tornar aquilo que é chamado de um superfluido. Neste artigo, vou guiá-lo pelo mundo fascinante dos superfluidos, apresentar algumas das coisas interessantes que eles fazem e explicar como esses materiais se relacionam com a descoberta que me levou a ganhar o Prêmio Nobel de Física em 2016.
O professor Michael Kosterlitz ganhou o Prêmio Nobel de Física em 2016, juntamente com os professores David Thouless e Duncan Haldane, pelas descobertas teóricas sobre transições de fase topológica e fases topológicas da matéria.
Topologia: uma linguagem matemática de formas
A topologia é o campo da matemática que estuda as formas das coisas e divide objetos em classes de acordo com essas formas. Um parâmetro-chave de qualquer forma é o número de furos que ela possui. Assim, por exemplo, uma esfera não tem furos, enquanto uma rosquinha tem um (Figura 1A). Portanto, uma esfera e uma rosquinha pertencem a duas classes topologicamente separadas. Isso significa que você não pode transformar facilmente uma esfera em uma rosquinha, pois teria que fazer um furo na esfera e, portanto, rasgar o material. Na topologia, você pode distorcer o material o quanto desejar, mas não pode fazer furos ou colar peças. Pode, sim, transformar uma esfera em uma tigela de sopa para que elas sejam topologicamente iguais. Isso talvez pareça muito estranho, mas tais ideias às vezes são úteis.
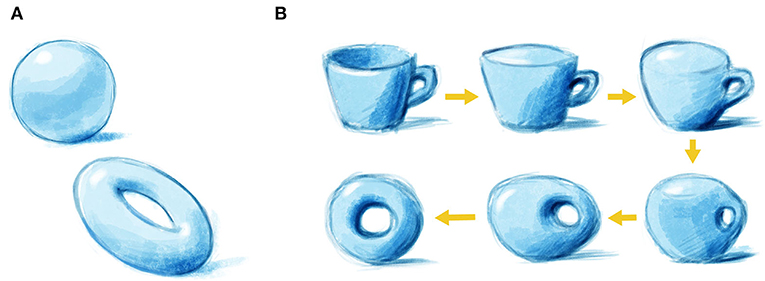
E quanto a uma rosquinha e uma xícara de café que possui uma alça? Elas podem parecer diferentes a princípio, mas se você olhar de perto verá que ambas têm um buraco. Na visão da topologia, isso significa que uma rosquinha e uma xícara de café são equivalentes. Para usar um termo técnico, têm equivalência topológica. Assim, você pode transformá-las uma na outra de maneira fácil e contínua (Figura 1B). Nesse caso, o número de buracos é chamado de invariante topológica – ele permanece o mesmo ou é preservado (invariante) em relação à rosquinha e à xícara de café, mesmo quando esses objetos passam por uma manipulação que altera sua aparência externa. A linguagem da topologia descreve as propriedades de certos materiais que são, por isso mesmo, chamados de materiais topológicos.
Na próxima seção, veremos como a topologia nos ajuda a identificar as diferenças entre os materiais e também a explicar certos fenômenos incomuns e excitantes, como fluidos que parecem desafiar a gravidade.
Materiais topológicos: dos simples aos exóticos
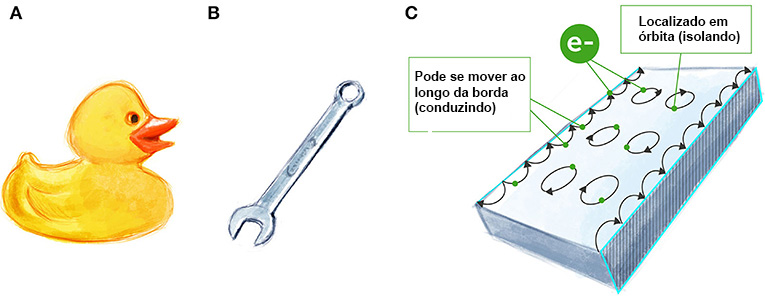
Como já mencionamos, a topologia é uma maneira conveniente de descrever certas diferenças observadas entre materiais. Uma família de materiais que todos conhecemos muito bem é a dos isolantes. Um isolante é um material que, como a borracha ou o plástico, não conduz facilmente a eletricidade. Essa propriedade é determinada pelas características energéticas do próprio material, ou seja, pelos níveis de energia gerados pelos elétrons nele presentes.
Usualmente, os materiais são caracterizados pela estrutura de suas faixas energéticas – os níveis de energia que podem ser ocupados pelos elétrons dentro de um dado material. No caso dos isolantes, existe uma “lacuna de energia” entre duas faixas energéticas que os elétrons normalmente não conseguem atravessar, de modo que seu movimento é limitado. Já no caso dos condutores, não há lacuna de energia e os elétrons ficam livres para se mover entre os níveis de energia dentro do material. O campo de energia de um sistema isolante pode ser classificado de acordo com as invariantes topológicas – propriedades topológicas que são preservadas mesmo quando o sistema muda seu estado. Isso significa que podemos identificar e classificar isolantes específicos com base nas propriedades topológicas de seus estados de energia.
Um grupo específico de isolantes atraiu muito interesse nos últimos quinze anos. Esses materiais são chamados de isolantes topológicos [1] porque podem ser classificados e descritos usando-se invariantes topológicas. Os isolantes topológicos são especiais porque conduzem e isolam ao mesmo tempo. Como pode ser isso? Na parte intermediária desses materiais, a qual é chamada de núcleo, os elétrons se movem em circuitos pequenos e fechados e não se deslocam (Figura 2C). Portanto, o núcleo dos materiais topológicos é isolante, como o plástico ou a borracha (Figura 2A). Mas, na superfície desses materiais, formam-se certos estados onde os elétrons podem se mover ao longo da borda (Figura 2C). Isso significa que as superfícies dos isolantes topológicos são condutoras, assim como os metais (Figura 2B).
Você pode estar pensando: “OK, isso é legal. Mas para que serve?” Essa pergunta ocupa hoje muitos físicos e engenheiros da computação. Vamos dar uma olhada em uma resposta possível.
Os isolantes topológicos são úteis?
Acontece que os estados condutores formados nas superfícies dos isolantes topológicos são muito estáveis – resistem a defeitos e perturbações do material. Uma das principais razões pelas quais esses estados são resistentes e estáveis é que suas características tendem a depender de todo o sistema – e não apenas de uma pequena parte dele ou de alguns átomos num local específico. Você pode imaginar esses estados como um fenômeno coletivo do material em sua totalidade. Ou seja, mesmo se algo pequeno – como uma imperfeição localizada – estiver presente no material, isso ainda não afetará significantemente nem alterará o estado topológico do sistema como um todo [2].
E qual a utilidade disso? A robustez de um isolante topológico é útil em aplicações computacionais, pois cria estabilidade. A estabilidade é o requisito mais fundamental de um elemento de computação (aquele que realiza cálculos), pois queremos que esses elementos forneçam resultados consistentes com o mínimo de erros possível.
Portanto, os isolantes topológicos têm um enorme potencial para melhorar os elementos de computação no futuro. No entanto, existem grandes desafios técnicos nesse processo e por isso ainda estamos muito longe de utilizar isolantes topológicos em computadores – o que certamente acontecerá no futuro. Agora vamos nos aprofundar um pouco mais no mundo encantado dos materiais topológicos e estudar minha contribuição para a explicação de um dos fenômenos mais exóticos da física, chamado superfluidez.
Um fluido voador: a história do hélio frio
Você sabia que existem fluidos capazes de desafiar a gravidade e escalar paredes de vidro? Eles são chamados de superfluidos e se comportam de maneira muito estranha em temperaturas extremamente baixas (a temperatura em que o hélio normal se torna hélio superfluido é chamada de temperatura de Transição Lambda, que é -56,15ºC à pressão de 1 atmosfera). Devido à sua natureza exótica, os superfluidos são de grande interesse para os cientistas. Eles nos permitem estudar fenômenos físicos excepcionais, que não encontramos na vida diária. O exemplo mais comum de superfluido é o hélio líquido, 4He. Você deve conhecer o hélio como o gás que enche os balões e faz as vozes das pessoas parecerem engraçadas quando o inalam, mas ele também pode existir como um líquido em temperaturas extremamente baixas, próximas do zero absoluto (-273°C).
Em 1972, três físicos publicaram uma experiência brilhante com películas de hélio [3]. Puseram um cristal de quartzo em uma atmosfera de gás hélio. Ajustando a pressão desse gás, eles alteraram a quantidade total de hélio adsorvido na superfície do cristal de quartzo, o que formou ali uma camada com dois ou três átomos de espessura. O cristal de quartzo possui uma frequência de vibração sonora natural, que depende da massa total do cristal vibratório. Quando uma fina camada de átomos de hélio fica presa (adsorvida) à superfície do cristal, espera-se naturalmente que esses átomos se movam com a superfície do cristal, de modo que seu único efeito será aumentar a massa do corpo vibratório e diminuir ligeiramente sua frequência sonora.
Quando os físicos mediram a frequência oscilatória do cristal coberto por uma camada muito fina de hélio, a baixa temperatura, obtiveram a diminuição esperada na frequência sonora. Porém, quando a pressão do gás e a cobertura de hélio foram aumentadas, a frequência sonora deixou de acompanhar a diminuição esperada (Figura 3A) e permaneceu diferente do valor que se esperava, como se o hélio extra houvesse se desprendido do movimento do cristal.
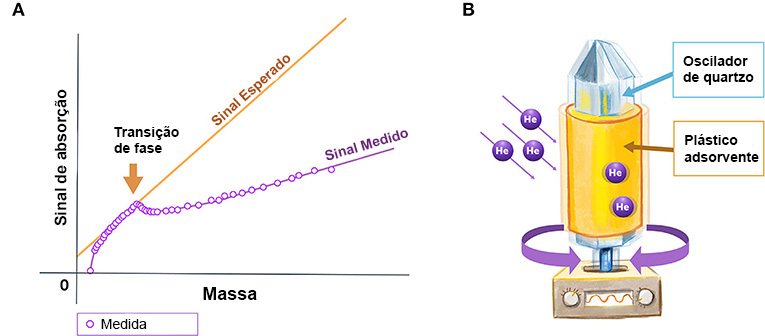
Mas se parte do hélio se torna um superfluido, ele não aumenta a massa do oscilador da mesma maneira, então a frequência oscilatória se reduz menos do que com o hélio normal (Adaptado de Chester et al. [3]). (B) Em um experimento posterior [4] com oscilações de frequência muito mais baixas, uma folha de plástico Mylar foi enrolada em uma haste osciladora torcional de quartzo, o gás 4He foi adsorvido na folha de Mylar e a frequência sonora e a dissipação foram medidas. O princípio desse experimento era o mesmo, mas chegou-se a resultados muito mais precisos e detalhados.
Em um experimento posterior, uma fita de plástico foi enrolada em uma haste osciladora feita de quartzo (Figura 3B). Quando você faz vibrar um quartzo semelhante a um cristal, ele apresenta uma frequência natural em que se move, chamada frequência oscilatória. Então, a primeira coisa que os físicos fizeram foi medir a frequência oscilatória natural da haste com o rolo de plástico ao seu redor. Em seguida, aumentaram a pressão do gás hélio em torno da haste osciladora e mediram novamente a frequência de oscilação da haste de quartzo.
Quando os átomos de hélio encontram a superfície do plástico adsorvente, eles normalmente o adsorvem (fixam), criando uma película ao redor da haste e aumentando sua massa. Como resultado, há uma ligeira redução na frequência oscilatória natural porque os cristais mais pesados oscilam em uma frequência mais baixa (movem-se mais lentamente) do que os cristais leves.
A maneira mais fácil de interpretar esse resultado era que parte da película de hélio não aderia mais ao oscilador quando ele se tornava um superfluido.
A diferença entre o hélio normal e o hélio superfluido se explica pela forma como eles fluem. O hélio normal se liga a tudo que tenta fluir, devido a uma propriedade chamada dissipação. O hélio superfluido, por outro lado, flui livremente sem dissipação e, portanto, parece “voar” ou pairar acima do material sobre o qual flui! Essa foi uma experiência pioneira, mostrando que películas de hélio tornam-se superfluidas a baixas temperaturas. O problema era que, até então, não tínhamos nenhuma teoria que pudesse explicar essa mudança no comportamento da película de hélio (chamada transição de fase), de normal para superfluido.
Na verdade, uma teoria comum na época sustentava até que tal transição de fase não deveria ocorrer sob essas condições e que a superfluidez era impossível numa película bidimensional. Portanto, essa experiência contradizia um princípio amplamente aceito sobre a natureza da fase de baixa temperatura de qualquer sistema.
Um teorema matemático rigoroso afirmava que a fase de baixa temperatura do sistema não poderia ter longo alcance em nenhuma temperatura – e isso significava, de acordo com o saber vigente, a impossibilidade de superfluidez em nossa película bidimensional. Agora tínhamos um grande conflito entre uma teoria rigorosa, segundo a qual a superfluidez numa película era impossível, e a observação experimental, que dizia exatamente o oposto. Claramente, ou a experiência ou a teoria deviam estar erradas ou mal interpretadas, pois a primeira mostrara inequivocamente que uma película de 4He é um superfluido e tem uma transição de fase.
Foi então que meu supervisor na época, o professor David Thouless, e eu entramos em cena: desenvolvemos uma nova teoria que explica a transição de fase de superfluido para fluido normal nas películas de hélio e resolvemos a contradição entre experimento e teoria.
Vórtices: “nos bastidores” do hélio superfluido
Como vimos, o hélio líquido tem duas fases. Em sua fase normal, ele flui com dissipação, isto é, interage com a superfície que encontra, troca energia com essa superfície e fica preso a ela. Em sua fase superfluida, o hélio líquido flui livremente, sem dissipação, e age como se estivesse pairando sobre a superfície que encontra. Para compreender a transição de fase entre o hélio normal e o superfluido, tivemos que investigar o mecanismo responsável pela dissipação.
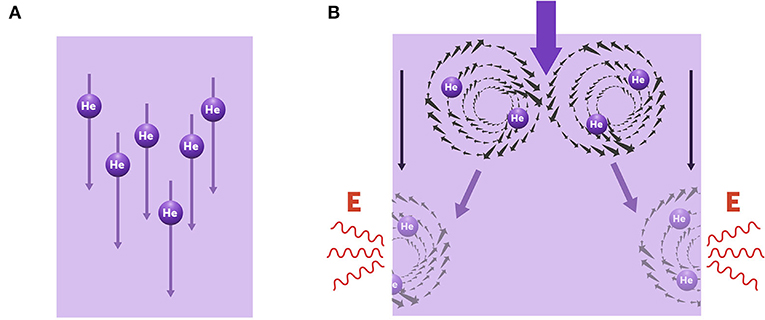
Descobrimos que a resposta estava em configurações peculiares chamadas vórtices (Figura 4), as quais, por razões de mecânica quântica, são as únicas excitações que podem dissipar o fluxo de um superfluido e explicar por que a superfície muito confusa de Mylar, onde o hélio está fluindo, não tem lugar nem na teoria nem no experimento. O único efeito do substrato está no atrito entre ele e os vórtices, o que não afeta o superfluido.
Para simplificar, você pode pensar no vórtice como um fluido circulando, como quando tira a tampa de uma banheira e a água gira enquanto desce pelo ralo. Para entender isso, terá de aprender muita física, então lembre-se de que esses vórtices no superfluido são as únicas excitações a serem consideradas e de que, em duas dimensões, esses vórtices interagem exatamente como partículas eletricamente carregadas: estas podem aparecer e desaparecer como quiserem, mas a carga total do sistema permanecerá zero.
Os vórtices se formam em pares neutros, um deles girando no sentido anti-horário e outro no sentido horário, em temperaturas muito baixas; todavia, em temperaturas mais altas, esses pares se desfazem em dois vórtices livres que derivam para as bordas do fluido e ali desaparecem, reduzindo assim o fluxo superfluido uniforme a uma pequena quantidade (Figura 4B). Essa é a dissipação vista no fluxo do fluido normal.
Dado que os dois estados do fluxo do hélio líquido podem ser definidos como dois estados topológicos, o hélio líquido também é considerado um material topológico – bem parecido com os isolantes topológicos que discutimos anteriormente .
Depois de descobrir que a física essencial do sistema superfluido pressupõe as interações de vórtices, elaboramos um modelo matemático para explicar a transição de fase do hélio líquido, bem como outras transições de fase em sistemas semelhantes, com altíssima precisão [4-7]. Esse foi um desenvolvimento importante, um grande passo à frente na compreensão de algumas das características intrigantes dos materiais topológicos.
Quero terminar com algumas informações pessoais para jovens leitores sobre minha paixão pela matemática e a física, e minhas recomendações para viverem uma vida feliz.
Recomendações para mentes jovens
Símbolos adoráveis: a beleza da matemática e da física
Quando fui apresentado à álgebra na escola, pensei comigo mesmo “Uau, essa é uma ótima maneira de fazer as coisas – muito melhor do que aritmética!”. É que a álgebra me permitia fazer muitas coisas em matemática que antes eu não podia fazer com facilidade. Foi como acender uma luz brilhante, que de repente tornou possível todo tipo de coisas!
Imediatamente gostei dos símbolos matemáticos, que eliminavam muita confusão e deixavam tudo bem simples. Sei que isso não acontece com todos, pois depende da forma de pensar de cada um. Mas, para mim, trabalhar com símbolos e equações é divertido e emocionante: gosto disso até hoje. De certa forma, para mim fazer física é semelhante a escalar montanhas (outra paixão minha): você está no desconhecido, sozinho, completamente responsável por seus atos, tentando seguir seu próprio caminho (Figura 5). A vantagem da física é que a punição por cometer um erro não é tão grave quanto na escalada!

Como escolher sua profissão
Você deve fazer aquilo de que gosta e aquilo em que é bom. É importante ser bom naquilo que faz porque, assim, gostará do que estiver fazendo. Também acho que deve se divertir com o que fizer, pois, caso não se divirta nem goste de seu trabalho, será inútil fazê-lo. Eis então o conselho que posso dar ao jovem leitor: divirta-se na vida porque você só têm uma e, se não se divertir, não valerá a pena viver.
Glossário
Topologia: Ramo da matemática que descreve as formas dos objetos.
Materiais topológicos: Materiais cujas propriedades são descritas pela topologia.
Isolantes topológicos: Materiais que exibem propriedades isolantes em seu núcleo e propriedades condutoras em suas superfícies.
Superfluidos: Fluidos que fluem sem dissipação.
Frequência de oscilação: ↑ Frequência na qual vibra um objeto chamado oscilador.
Dissipação: Perda de energia que não pode ser revertida sem adição de energia externa.
Transição de fase: Mudança abrupta entre dois estados de um sistema, fazendo com que as propriedades desse sistema se alterem. Por exemplo, a transição da água líquida para o gelo sólido.
Conflito de interesses
O autor declara que a pesquisa foi realizada sem nenhuma relação financeira ou comercial capaz de gerar um conflito de interesses.
Agradecimentos
Agradeço a Noa Segev por conduzir a entrevista que serviu de base para este artigo e por sua coautoria, a Alex Berstein por fornecer as ilustrações e a Susan Debad por preparar o manuscrito. Obrigado ao dr. Subramanian Ramachandran por seus valiosos comentários sobre o texto.
Referências
[1] Moore, J. E. 2010. “The birth of topological insulators.” Nature. 464:194–8. DOI: 10.1038/nature08916.
[2] Qi, X. L. e Zhang, S. C. 2010. “The quantum spin hall effect and topological insulators.” arXiv preprint.arXiv: 1001.1602. DOI: 10.1063/1.3293411.
[3] Chester, M., Yang, L. C. e Stephens, J. B. 1972. “Quartz microbalance studies of an adsorbed helium film.” Phys. Rev. Lett. 29:211. DOI: 10.1103/PhysRevLett.29.211.
[4] Bishop, D. J. e Reppy, J. D. 1978. “Study of superfluid transition in 2-dimensional 4He films.” Phys. Rev. Lett. 40:1727. DOI: 10.1103/PhysRevLett.40.1727.
[5] Kosterlitz, J. M. e Thouless, D. J. 1973. “Ordering, metastability and phase transitions in two-dimensional systems.” J. Phys. C Solid State Phys. 6:1181. DOI: 10.1088/0022-3719/6/7/010.
[6] Kosterlitz, J. M. 2016. “Kosterlitz-Thouless physics: a review of key issues.” Rep. Prog. Phys. 79:026001. DOI: 10.1088/0034-4885/79/2/026001.
[7] ↑ Hadzibabic, Z., Krüger, P., Cheneau, M., Battelier, B. e Dalibard, J. 2006. “Berezinskii-Kosterlitz-Thouless crossover in a trapped atomic gas.” Nature. 441:1118–21. DOI: 10.1038/nature04851.
Citação
Kosterlitz, M. (2023). “Defying gravity? On the magic tricks of superfluids.” Front. Young Minds. 11:1039653. DOI: 10.3389/frym. 2022.1039653.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br