Como usar a matemática para estudar as influências que as pessoas exercem sobre as opiniões umas das outras
Autores
Grace J. Li, Jiajie (Jerry) Luo, Kaiyan Peng, Mason A. Porter
Jovens revisores
Resumo
Às vezes, quando discutem umas com as outras, as pessoas mudam de opinião. Os pesquisadores podem usar a matemática para estudar mudanças de opinião em simplificações de situações da vida real. Estes cenários simplificados, que são exemplos de modelos matemáticos, ajudam os investigadores a explorar o modo como as pessoas influenciam umas às outras através das suas interações sociais. No mundo digital de hoje, estes modelos podem ajudar-nos a aprender como promover a difusão de informações precisas e reduzir a difusão de informações imprecisas. Neste artigo, discutimos um modelo matemático simples de mudanças de opinião que surgem das interações sociais. Descrevemos brevemente o que os modelos de opinião podem nos dizer e como os pesquisadores tentam torná-los mais realistas.
Como os pesquisadores estudam as mudanças de opinião?
No romance “Ad Eternum”, de Elizabeth Bear, uma personagem comenta: “As opiniões são como gatinhos. As pessoas estão sempre doando”.
Todo mundo tem opiniões. Nossas opiniões sobre as coisas mudam com o tempo e muitas vezes são influenciadas pelas opiniões de outras pessoas. Muitos pesquisadores estudam como as opiniões mudam com o tempo e como as pessoas influenciam umas às outras [1, 2]. Eles utilizam frequentemente a matemática para investigar estas ideias e obter conhecimentos sobre como as pessoas mudam os seus pontos de vista, como grupos de pessoas formam opiniões partilhadas e como essas opiniões partilhadas mudam.
Imagine que sua escola está redesenhando seu logotipo e cores. O diretor da escola anunciou que a administração selecionou duas cores possíveis – vermelho e azul – e que os alunos podem votar em qual dessas duas cores se tornará a cor principal da escola. Durante o intervalo do almoço, você e seus amigos estão sentados à mesa discutindo as novas opções de cores. Suponha que apenas duas pessoas discutam as opções de cores por vez. Suponha também que sua preferência seja vermelha. Você recorre a um de seus amigos para discutir as cores da escola. Seu amigo diz que o azul ficaria melhor em camisas escolares e convence você a preferir o azul. Depois, outro amigo vem a você discutir o assunto, e você o convence a também preferir o azul. Imagine que essas discussões entre colegas continuam até que, eventualmente, todos na mesa do almoço sejam convencidos a preferir a mesma cor.
Podemos estudar o processo de discussão acima usando um modelo matemático, que é uma descrição de algo usando regras matemáticas e linguagem. Um exemplo é um modelo de opiniões e como elas mudam [3].
Os pesquisadores usam modelos matemáticos para investigar como as opiniões mudam devido às interações sociais, como aquelas nas conversas dos alunos no almoço. Os pesquisadores frequentemente estudam modelos simples que são fáceis de entender e explorar. Um modelo que os pesquisadores usam para situações como a acima é chamado de modelo de eleitor. Um modelo de opinião em que se escolhe repetidamente pares aleatórios de pessoas (ou outros indivíduos) para concordar com uma de suas opiniões. Existem muitas variações de modelos de eleitor (que, apesar do nome, quase nada tem a ver com votação) [3].
Os modelos eleitorais têm dois ingredientes principais: (1) as opiniões iniciais das pessoas, que é o que elas pensam antes de discutirem as suas opiniões com outras pessoas; e (2) uma regra de atualização: uma regra que determina como as pessoas mudam suas opiniões em um modelo de opinião. Uma regra de atualização determina como as pessoas interagem entre si e como elas mudam suas opiniões quando interagem, o que descreve como as opiniões das pessoas mudam.
No nosso exemplo, as opiniões iniciais são as cores (vermelho ou azul) que cada pessoa prefere inicialmente. Para a regra de atualização neste modelo de eleitor, escolhemos aleatoriamente duas pessoas e, em seguida, escolhemos aleatoriamente uma de suas opiniões para que elas concordem após a discussão. Cada uma das duas opiniões é igualmente provável. (Imagine jogar uma moeda para determinar com qual opinião concordar.) Se ambas as pessoas já tiverem a mesma opinião, ainda podemos escolhê-las para discutir suas opiniões entre si. No entanto, nesse caso, as opiniões de ambos permanecem as mesmas.
Esta regra de atualização imita uma discussão em que uma pessoa pode convencer outra a mudar sua preferência de cor. Esta simples regra de atualização não captura os muitos detalhes de como as pessoas interagem na vida real. (Por exemplo, esta regra não inclui memória de quaisquer discussões anteriores.) No entanto, apesar da natureza ingênua da regra, ainda ajuda os investigadores a estudar como as opiniões das pessoas mudam com o tempo.
Na Figura 1, você pode ver como um modelo de eleitor se relaciona com nosso exemplo de amigos discutindo suas cores preferidas na escola durante o almoço. Quando todos concordam com a mesma cor, chegaram a um consenso (quando todos têm a mesma opinião, dizemos que chegaram a um consenso). Quando as pessoas não estão em consenso, dizemos que têm opiniões fragmentadas (um grupo de pessoas tem opiniões fragmentadas quando não estão em consenso). Existem duas ou mais opiniões diferentes. Por exemplo, quando as pessoas estão polarizadas com duas opiniões diferentes (como vermelho ou azul para a cor da escola), as suas opiniões são fragmentadas. Num modelo de eleitor, os investigadores estão interessados em saber se as pessoas eventualmente chegam a um consenso e, em caso afirmativo, quanto tempo leva para alcançá-lo [2].
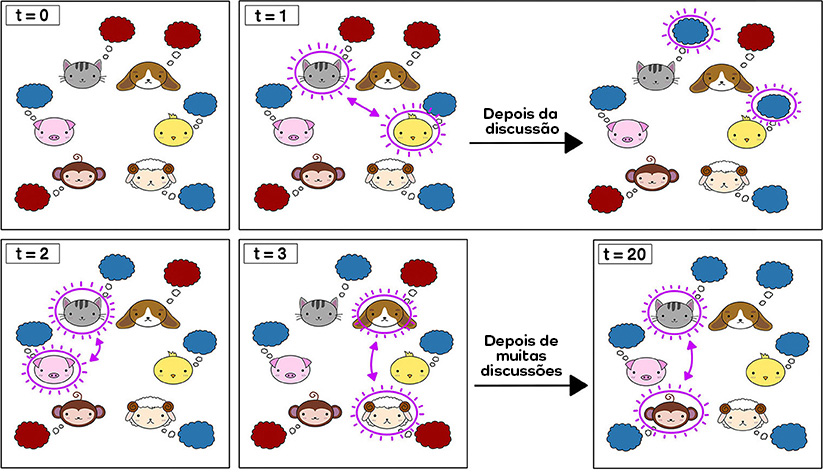
Inicialmente (no tempo t = 0), cada animal prefere o azul ou o vermelho como cor principal do cardume. No tempo t = 1, Pássaro e Gato discutem as cores da escola e decidem que preferem o azul. No tempo t = 2, Gato e Porco discutem as cores da escola. Eles preferem a mesma cor, por isso suas opiniões não mudam. No tempo t = 3, Cão e Ovelha discutem as cores da escola e decidem que preferem o vermelho. As atualizações de opinião continuam até que os animais cheguem a um consenso. Neste exemplo, no tempo t = 20, Todos preferem o azul.
Incorporando Redes Sociais em Modelos de Opinião
Em nosso exemplo das cores da escola, um pequeno grupo de amigos discute suas preferências de cores em pares. Suponha que essas discussões ocorram numa grande escola onde nem todos os alunos se conhecem. Os pesquisadores podem representar o conjunto de relações sociais em uma escola como uma rede social – um conjunto de pessoas e as relações sociais entre elas.
Exemplos de relacionamentos sociais incluem amizades, relacionamentos familiares e conexões de mídia social dos alunos. Os alunos são os “nós” da rede social (um é um objeto em uma rede social que representa uma pessoa ou outro indivíduo. Dois nós que possuem uma aresta entre eles são chamados de “vizinhos”), e as relações sociais que conectam os alunos são as arestas – uma conexão entre dois nós em uma rede social. Uma aresta da rede pode representar uma amizade ou algum outro relacionamento social. Se duas pessoas mantêm uma relação social, dizemos que são “vizinhos” na rede. Em nosso exemplo, os nós terão arestas entre eles se forem amigos.
Quando os investigadores estudam um modelo de eleitor numa rede social, apenas os nós vizinhos podem influenciar as opiniões uns dos outros. Ou seja, assumem que apenas as pessoas com relacionamento social influenciam-se diretamente. Por exemplo, os alunos de uma escola tendem a influenciar os amigos. A utilização das redes sociais permite aos investigadores estudar como a estrutura da rede – isto é, quem é amigo de quem – influencia as mudanças de opinião.
Considere uma rede social de amizades entre alunos de uma escola. Vejamos nosso modelo de eleitor nesta rede social. Como antes, cada aluno inicialmente prefere o vermelho ou o azul. No entanto, ao contrário do nosso exemplo sem rede social, algumas pessoas não são amigas umas das outras. Duas pessoas só discutem suas preferências se forem amigas. A cada atualização do modelo, escolhemos aleatoriamente uma dupla de amigos para conversar; ou seja, escolhemos vizinhos na rede social dos alunos. Em seguida, escolhemos aleatoriamente uma de suas opiniões e supomos que ambos os alunos concordam com essa opinião após a discussão. Como antes, esta atualização de opinião representa uma pessoa convencendo seu amigo a preferir a mesma cor que ela.
Na Figura 2 você pode ver um exemplo de como esse modelo de eleitor é atualizado em uma rede social muito pequena. As opiniões mudam com o tempo e, eventualmente, todos os alunos concordarão em votar na mesma cor. Ou seja, os alunos acabarão por chegar a um consenso. Infelizmente, na vida real, pode demorar muito tempo para chegar a um consenso; uma escola pode não esperar tanto tempo para decidir uma cor. Para examinar situações como esta, os investigadores estudam como as opiniões num modelo de eleitor mudam num determinado período de tempo (como uma semana) para ver se surge um consenso. Os pesquisadores também estudam quanto tempo leva para surgir um consenso.
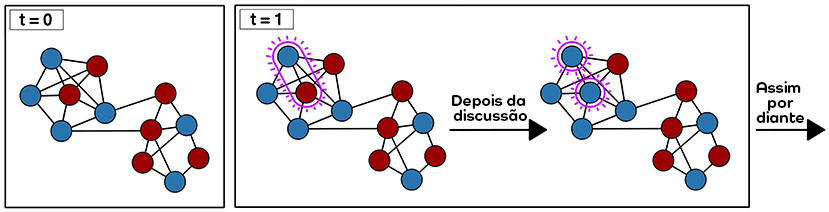
As pessoas (os nós) são círculos preenchidos e suas amizades (as arestas) são linhas pretas que conectam os nós. Colorimos os nós de acordo com sua opinião (azul ou vermelho). No tempo t = 0, mostramos a rede social e as opiniões iniciais de todos. Ao contrário da Figura 1, apenas amigos (ou seja, nós vizinhos) podem interagir; algumas pessoas são amigas umas das outras, mas outras não. A cada momento, selecionamos aleatoriamente dois amigos para interagir e atualizar suas opiniões.
Ao estudar um modelo de eleitor, uma escolha possível é determinar aleatoriamente as opiniões iniciais dos nós. No entanto, em nosso exemplo, as preferências iniciais de cores provavelmente não vêm de um processo aleatório como jogar uma moeda. Muitas pessoas preferem certas cores e não gostam de outras. Essas preferências podem surgir por vários motivos. Talvez alguém use frequentemente roupas azuis ou tenha um time esportivo favorito que tenha o azul como cor.
Uma pessoa também pode querer evitar uma cor que corresponda à cor de um time esportivo rival. Numa rede social escolar, existem comunidades de pessoas com muitas amizades dentro da comunidade. Por exemplo, comunidades de amizade podem surgir de turmas, clubes escolares ou equipes esportivas. Pessoas na mesma comunidade têm maior probabilidade de serem amigas umas das outras do que pessoas em comunidades diferentes.
Como você pode ver na Figura 3, os pesquisadores podem escolher opiniões iniciais com base nessas comunidades. Por exemplo, suponha que a cor do time de futebol local seja azul. Talvez mais alunos da 7ª série do que da 8ª série sejam fãs do time, então talvez os alunos da 7ª série sejam mais propensos do que os da 8ª série a preferir o azul como cor principal da escola. Os pesquisadores estudam como as comunidades nas redes sociais afetam o resultado dos modelos eleitorais e, de forma mais geral, como influenciam as opiniões das pessoas. Será que as pessoas numa rede social acabarão por chegar a um consenso? Se sim, quanto tempo levará?
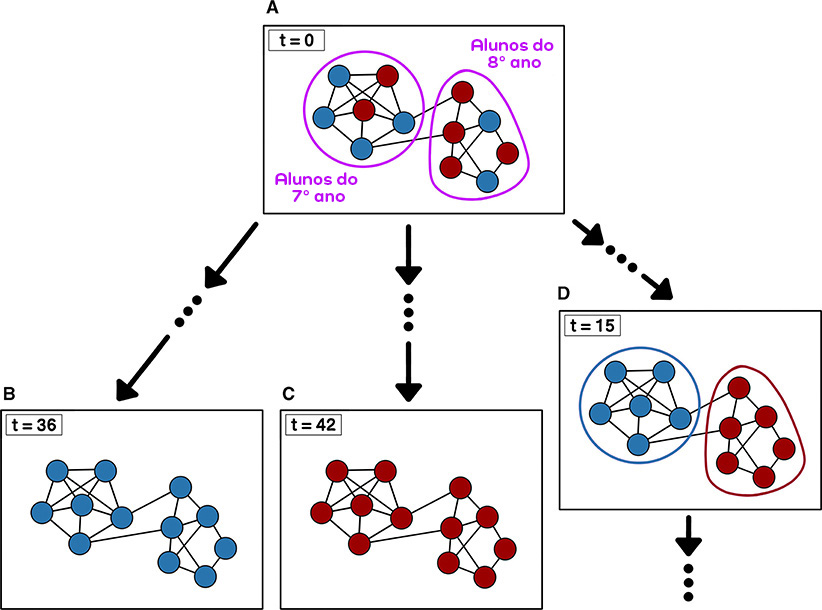
Considere uma rede social com duas comunidades – alunos do 7º ano e do 8º ano – que tendem a preferir o azul e o vermelho, respetivamente. (A) No tempo t = 0, selecionamos qual cor cada aluno prefere. Usando essas mesmas preferências iniciais, simulamos o modelo do eleitor diversas vezes em um computador. (B) Em uma simulação, todos os alunos eventualmente preferiram o azul. (C) Em outra simulação, todos os alunos eventualmente preferem o vermelho. (D) Em outra simulação, as duas comunidades ainda têm preferências diferentes no tempo t = 15. Continuamos esta simulação até que todos os alunos cheguem a um consenso.
Os modelos de opinião geralmente incluem aleatoriedade. Num modelo de eleitor, a aleatoriedade resulta da escolha das opiniões iniciais, da determinação de qual par específico de pessoas interage em cada momento e da determinação de qual opinião essas pessoas concordam. Na Figura 3, você pode ver que a aleatoriedade pode fazer com que exatamente o mesmo modelo matemático forneça resultados diferentes. Os investigadores precisam ter cuidado ao determinar se as diferenças nos resultados dos modelos surgem de características (como comunidades) de redes sociais ou de aleatoriedade. Eles utilizam frequentemente simulações computacionais para estudar modelos de opinião, e é importante simular um modelo (como um modelo eleitoral) muitas vezes para explorar cuidadosamente os seus possíveis resultados.
O que podemos aprender com os modelos eleitorais?
Por que os investigadores estão interessados em modelos de eleitores e outros modelos de opinião? Decidir sobre as novas cores da escola pode não parecer grande coisa. No entanto, o estudo dos modelos de opinião também pode ajudar os investigadores a examinar as mudanças nas opiniões públicas sobre temas importantes como as eleições presidenciais e as políticas de vacinação. Os modelos de opinião podem fornecer informações sobre como promover a divulgação de informações precisas e como o uso das mídias sociais pode afetar nossos pontos de vista [4].
A mídia social mudou a forma como as pessoas interagem e como as opiniões se espalham. Por exemplo, influenciou a opinião das pessoas sobre a COVID-19 [4]. As redes sociais podem ajudar as autoridades de saúde a compartilhar orientações importantes, como informações sobre vacinas. Infelizmente, as redes sociais também podem ajudar a espalhar informações falsas e enganosas, que podem prejudicar a saúde física e mental de muitas pessoas.
Pesquisadores de muitas disciplinas – incluindo matemática, psicologia, sociologia, biologia, física, economia, ciência da computação e outras – estudam modelos de opinião por vários motivos [5]. Matemáticos e físicos frequentemente estudam esses modelos porque são interessantes. Cientistas políticos usaram modelos de opinião para estudar a polarização e os resultados das votações nas eleições [1, 5]. Nos negócios, modelos de opinião têm sido usados para estudar decisões de preços nos mercados financeiros, análises de produtos em vendas online e os efeitos de campanhas publicitárias [6]. Os pesquisadores também examinaram como as mudanças de opinião e a propagação de doenças se afetam mutuamente, estudando modelos que as combinam [4].
Os modelos de eleitor têm muitas aplicações e podemos torná-los mais úteis tornando-os mais realistas. Como podemos tornar os modelos de eleitores mais realistas? Em um modelo de eleitor, selecionamos aleatoriamente qual opinião é compartilhada por dois indivíduos após eles interagirem. Contudo, na realidade, não está claro como as pessoas formam e mudam as suas opiniões.
As opiniões das pessoas também são influenciadas por outros fatores além da influência direta de outras pessoas. Formar e mudar opiniões são processos complicados, por isso são difíceis de modelar matematicamente. A regra de atualização do nosso modelo de eleitor simplifica demais a realidade, por isso os pesquisadores tentaram tornar essas regras mais realistas [1, 3]. Os investigadores também desenvolveram muitos outros tipos de modelos de opinião – tais como modelos que incluem pessoas teimosas que provavelmente não mudarão as suas opiniões – para incorporar várias ideias de como as pessoas mudam as suas opiniões [1, 2]. Eles também desenvolveram modelos de opinião que incorporam noções de pressão dos pares [3].
Por exemplo, talvez algumas pessoas apenas mudem de opinião para uma opinião que seja suficientemente popular entre os seus amigos (por exemplo, quando pelo menos cinco dos seus amigos têm essa opinião). Os pesquisadores também estudam modelos de opinião nos quais a estrutura das redes sociais e as opiniões mudam de maneiras que dependem umas das outras [7]. Por exemplo, talvez você pare de seguir uma pessoa no TikTok ou Instagram se discordar fortemente sobre um assunto importante.
Resumo e para onde ir a partir daqui
Estudar como as interações sociais entre as pessoas afetam suas opiniões é uma maneira fascinante de usar a matemática. Os pesquisadores criam novos modelos de opinião para desenvolver insights sobre as interações humanas e seus efeitos nos fenômenos sociais. Esses modelos são muito mais simples do que a forma como as opiniões mudam na realidade. Um grande desafio na modelagem de opiniões é avaliar modelos comparando-os com opiniões em dados do mundo real [1]. Os pesquisadores estão tentando ativamente desenvolver formas eficientes para fazer isso.
No entanto, apesar dos desafios, os modelos de opinião ainda ajudam os investigadores a testar e aprender como as interações sociais afetam as nossas opiniões. À medida que os investigadores desenvolvem mais modelos de opinião, aprenderemos mais sobre como as opiniões mudam e como essas mudanças impactam o comportamento humano.
Glossário
Modelo Matemático: Uma descrição de algo usando regras matemáticas e linguagem. Um exemplo é um modelo de opiniões e como elas mudam.
Modelo de eleitor: Um modelo de opinião em que se escolhe repetidamente pares aleatórios de pessoas (ou outros indivíduos) para concordar com uma de suas opiniões. Existem muitas variações de modelos de eleitor.
Regra de atualização: Uma regra que determina como as pessoas mudam suas opiniões em um modelo de opinião. Uma regra de atualização determina quais pessoas interagem entre si e como elas mudam suas opiniões quando interagem.
Consenso: Quando todos têm a mesma opinião, dizemos que chegaram a um consenso.
Opiniões fragmentadas: Um grupo de pessoas tem opiniões fragmentadas quando não há consenso. Existem duas ou mais opiniões diferentes.
Rede Social: Um conjunto de pessoas e as relações sociais entre elas. Exemplos de relacionamentos sociais incluem amizades, relacionamentos familiares e conexões de mídia social.
Nó: Um objeto em uma rede social que representa uma pessoa ou outro indivíduo. Dois nós que possuem uma aresta entre eles são chamados de “vizinhos”.
Aresta: Uma conexão entre dois nós em uma rede social. Uma aresta pode representar uma amizade ou algum outro relacionamento social.
Referências
[1] Peralta, A. F., Kertész, J., e Iñiguez, G. 2022. “Opinion dynamics in social networks: From models to data,” to appear in Handbook of Computational Social Science, in press, ed. T. Yasseri (Cheltenham, Reino Unido: Edward Elgar Publishing Ltd), arXiv:2201.01322.
[2] Noorazar, H., Vixie, K. R., Talebanpour, A., e Hu, Y. 2020. From classical to modern opinion dynamics. Int. J. Mod. Phys. C. 31:2050101. doi: 10.1142/S0129183120501016
[3] Redner, S. 2019. Reality-inspired voter models: A mini-review. Comp. Rend. Phys. 20:275–92. doi: 10.1016/j.crhy.2019.05.004
[4] Bedson, J., Skrip, L. A., Pedi, D., Abramowitz, S., Carter, S., Jalloh, M. F., et al. 2021. A review and agenda for integrated disease models including social and behavioural factors. Nat. Hum. Behav. 5:834–46. doi: 10.1038/s41562-021-01136-2
[5] Galesic, M., Olsson, H., Dalege, J., van der Does, T., e Stein, D. L. 2021. Integrating social and cognitive aspects of belief dynamic: Towards a unifying framework. J. R. Soc. Interf. 18:20200857. doi: 10.1098/rsif.2020.0857
[6] Zha, Q., Kou, G., Zhang, H., Liang, H., Chen, X., Li, C.-C., et al. 2020. Opinion dynamics in finance and business: A literature review and research opportunities. Finan. Innovat. 6:44. doi: 10.1186/s40854-020-00211-3
[7] Berner, R., Gross, T., Kuehn, C., Kurths, J., e Yanchuk, S. 2023. Adaptive dynamical networks. Phys. Rep. 1031:1–59. doi: 10.1016/j.physrep.2023.08.001
Citação
Li GJ, Luo J(, Peng K e Porter MA (2024) Using Mathematics to Study How People Influence Each Other’s Opinions. Front. Young Minds. 12:1253153. doi: 10.3389/frym.2024.1253153
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br


