Ligando os pontos: como descobrir a “forma” dos dados
Autores
Abigail Hickok, Chad M. Topaz, Mason A. Porter, Michelle Feng, Yacoub H. Kureh
Jovens revisores

Resumo
Cientistas usam um recurso chamado topologia para estudar as formas dos objetos. Uma parte importante da topologia é a contagem do número de peças e de orifícios em um objeto, informações que os cientistas usam para agrupar objetos em diferentes tipos. Por exemplo, uma rosquinha tem o mesmo número de furos e o mesmo número de peças que uma xícara com uma alça, mas é diferente de uma bola. Em estudos que lembram atividades como “ligue os pontos”, os cientistas aproveitam ideias da topologia para estudar a “forma” dos dados. Ideias e métodos da topologia têm sido usados para investigar as estruturas ramificadas de nervuras em folhas, a votação em eleições, os padrões de voo em modelos de bandos de pássaros etc.
O que é uma forma?
As formas são tão fundamentais em nossa existência que nosso cérebro começa a notá-las quando temos apenas 4 ou 5 meses de vida. Mas o que, exatamente, queremos dizer com “forma”? Estamos habituados a descrever formas comuns como linhas, círculos e cubos; mas o que dizer de objetos mais complicados como um dragão, um Pokémon ou um ser humano?
A topologia é um ramo da matemática que se ocupa das formas das coisas [1, 2]. Para entender melhor a topologia, vamos imaginar que temos uma tira de borracha circular. Queremos descrever as propriedades de um objeto que permaneça o mesmo quando esticado, encolhido ou encurvado, mas sem quebrá-lo ou colar partes. Do ponto de vista topológico, como podemos esticar a tira dando-lhe a forma oval, dizemos que o círculo e o oval são topologicamente equivalentes. No entanto, a tira de borracha não é topologicamente equivalente a um segmento de barbante, pois a tira tem um orifício no meio e o barbante, não. Lembre-se de que não podemos colar as pontas do barbante nem cortar a tira de borracha.
Para descobrir quais formas são equivalentes nesse caso especial, separamos as formas em grupos diferentes. Por exemplo: vamos agrupar as letras da palavra “Pokémon” em grupos de objetos topologicamente equivalentes. (Veja a curta animação no Vídeo 1.) As letras “P” e “o” pertencem ao mesmo grupo porque podemos comprimir a parte inferior do “P” para cima e depois esticar o orifício, dando-lhe a forma da letra “o”. Portanto, “P” e as duas letras “o” constituem um grupo de letras topologicamente equivalentes. O “k”, o “m” e o “n” entram num grupo diferente, já que podemos transformar cada um deles em um ponto ao espremê-los e encurvá-los.
A letra restante, “e”, é bem interessante. Ignorando o acento, conseguiríamos encurtar seu “rabinho” arredondado para o lado esquerdo do semicírculo, no alto da letra; em seguida, esticaríamos o semicírculo e obteríamos a letra “o”, o que a colocaria no mesmo grupo do “P” e do “o”. Entretanto, por causa do acento, “é” possui duas peças separadas, que não podemos colar – então, essa letra tem seu próprio grupo.
Formas de um mesmo grupo têm traços importantes em comum. Embora os detalhes das formas “P” e “o” sejam diferentes, as duas possuem um orifício que não podemos remover. Já as letras “k”, “m” e “n” não têm orifícios. Se observarmos a letra “B” (maiúscula), percebemos que ela não pertence a nenhum desses grupos. No entanto, é topologicamente equivalente ao número “8” porque ambos possuem dois orifícios. O número de peças em um objeto também é importante, portanto, o “é” (com um orifício e duas peças) não pertence a nenhum dos grupos de letras que vimos até agora. Tente separar as letras de seu nome em grupos de letras topologicamente equivalentes.
Agora, vamos deixar as coisas ainda mais interessantes olhando para alguns Pokémons. Para cada Pokémon na Figura 1, conte o número de peças e orifícios. Você é capaz de agrupar alguns deles com base nessa informação?

Talvez seja difícil estudar a topologia de objetos sólidos como os que vimos até agora, mas que tal criar imagens utilizando técnicas como “ligue os pontos”? Frente a uma grande quantidade de pontos, quase sempre conseguimos imaginar a forma que terão quando ligados (ver Figura 2). Normalmente, as pessoas têm facilidade para descobrir as formas com base apenas nesses pontos – mas haverá um modo de fazer isso automaticamente? Embora tal tipo de atividade seja, em geral, mais difícil para um computador do que para um humano, matemáticos e outros cientistas buscam meios de realizar essa tarefa de maneira automática porque queremos olhar para muitas coleções diferentes de pontos.

A topologia nos ajuda a dar sentido a grandes quantidades de dados. Podemos imaginar a exploração da topologia de uma coleção de dados (chamada conjunto de dados) como um gigantesco jogo de “ligue os pontos”. Na vida real, existem inúmeros tipos diferentes de dados, que talvez não apresentem a forma de pontos numa página. Contudo, trabalharemos com dados que também possuem números associados, como as populações e outros aspectos de regiões em mapas, a altura dos estudantes em uma escola ou a quantidade de palavras em cada parágrafo deste artigo. Podemos analisar dados desse tipo de maneira parecida à como pensamos em pontos numa página.
Como descobrir a forma de dados
Pensar conjuntamente em topologia e dados constitui uma área de estudo chamada análise topológica de dados (TDA) [3, 4, 5]. Na TDA, tentamos descrever a forma de um conjunto de dados elaborando uma série de imagens. Ligando os “pontos” num conjunto de dados, de várias formas diferentes, podemos estudar a estrutura desses dados. Em vez de ligar os pontos traçando linhas de um a outro, como costumamos fazer, podemos ligá-los aumentando seu tamanho. Quando aumentamos o tamanho dos pontos, o espaço entre eles fica menor e eles acabam se sobrepondo (ver Figura 3).
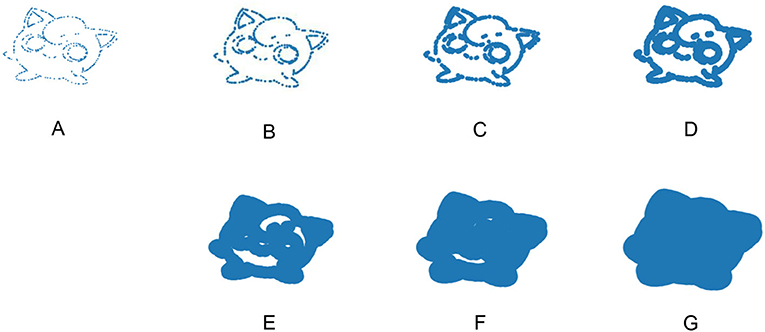
É importante saber que tamanho daremos aos pontos. O que vai acontecer se fizermos os pontos muito grandes, como na Figura 3G? Teremos um objeto enorme, sem orifícios. Nesse exemplo, quase não conseguimos distinguir Jigglypuff porque os pontos são muito grandes. Detalhe importante, talvez percebamos coisas interessantes por causa do tamanho diferente dos pontos. Usando matemática e computação, podemos considerar diversos tamanhos de pontos e criar um objeto para cada um deles. Cada uma das sete versões de Jigglypuff na Figura 3 possui um número diferente de peças e orifícios, que podemos contar (Tabela 1).
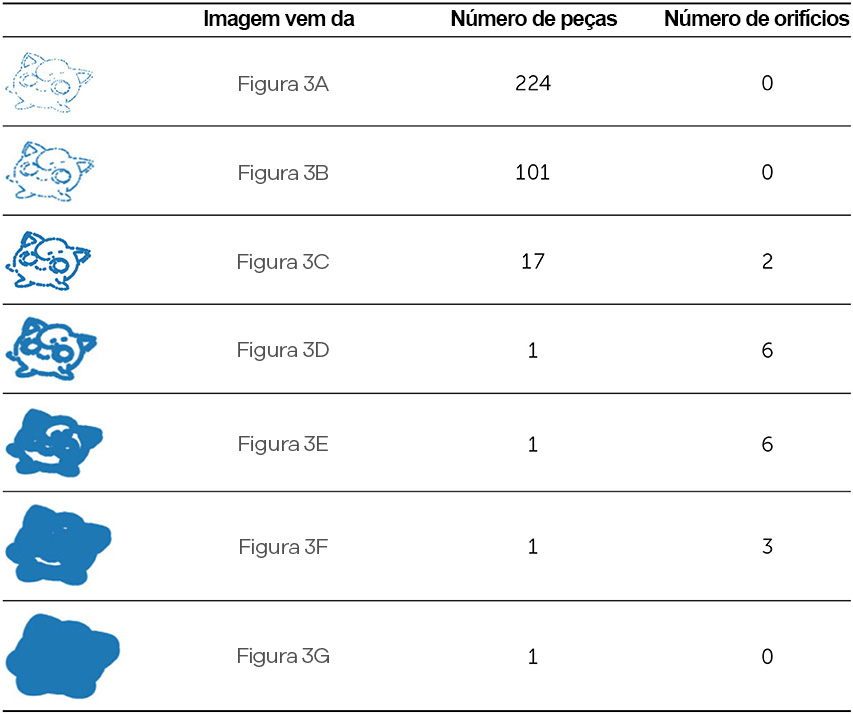
Tabela 1. Podemos descrever as sete imagens de Jigglypuff na Figura 3 com os seguintes pares de números: (224, 0), (101, 0), (17, 2), (1, 6), (1, 6), (1, 3) e (1, 0). Em cada par, o primeiro valor indica o número de peças e o segundo indica o número de orifícios.
A informação na Tabela 1 é uma das maneiras de descrever e resumir o que aprendemos com o estudo dessa série de tamanhos de pontos. Ou seja, estudamos a estrutura de Jigglypuff em diversos tamanhos (escalas). Cada versão dele na Figura 3 está numa escala; contando o número de peças e orifícios em cada escala, conseguimos explorar a série de tamanhos dos pontos em que os traços de Jigglypuff persistem. Essa é uma abordagem comum em TDA: observamos o tamanho dos pontos em que diferentes traços persistem nos dados que queremos estudar.
O que podemos aprender com a análise topológica de dados?
A TDA pode nos dizer muita coisa sobre o que existe no mundo. Ela nos permite explorar dados complexos de uma enorme variedade de tópicos em ciência social, biologia, astronomia etc. [3].
Podemos usar a TDA para ter uma melhor compreensão do universo. Planetas como a Terra são parte de sistemas solares que, por sua vez, são parte de galáxias, que existem em aglomerados. Se olharmos por um telescópio e dermos um zoom em um sistema solar, os planetas parecerão muito afastados uns dos outros. Mas, se diminuirmos o zoom para olhar galáxia inteira, cada sistema solar parecerá um simples ponto, com suas estruturas internas fundidas. Se diminuirmos ainda mais o zoom, cada galáxia também parecerá um simples ponto. A fim de estudar a estrutura do universo nessas diferentes escalas, cientistas usam a TDA para contar a quantidade de peças e orifícios em um conjunto de dados das posições das estrelas [6].
De volta à Terra, cientistas recorrem à TDA para examinar os padrões de nervuras em folhas [7]. Eles já estudaram a estrutura de mais de cem folhas e encontraram diferentes padrões – algo semelhante às digitais humanas. Essas “digitais” podem ajudar os cientistas a identificar folhas a partir de alguns de seus fragmentos menores e a entender melhor como elas crescem. A TDA também é útil para o estudo da estrutura dos fungos, vasos sanguíneos e outras coisas que possuem ramificações e entrelaçamentos.
A TDA também é utilizada na descrição de padrões de atividade de pessoas e animais. Por exemplo, dois de nós estudamos recentemente os padrões geográficos de votação em diferentes regiões da Califórnia [8]. Nós usamos a TDA para detectar áreas do estado em que os eleitores votaram de maneira diferente do que em outras áreas vizinhas na eleição presidencial de 2016. Cardumes e bandos de pássaros incluem numerosos indivíduos e formam belas estruturas. A TDA ajuda os cientistas na investigação e compreensão desses padrões complexos [9].
Em suma, a TDA é uma abordagem cada vez mais popular no estudo de diversos problemas, que vão desde ligar pontos em imagens de Pokémon até a estrutura do universo [6], padrões da natureza [7], padrões geográficos de votação em eleições [8] e muito mais. A TDA é uma fascinante e importante área da matemática que ajuda as pessoas a compreenderem dados complexos [3, 4, 5].
Glossário
Topologia: Ramo da matemática usado no estudo das formas de objetos.
Topologicamente equivalente: Expressão usada para descrever dois objetos que podem ser convertidos um no outro quando os esticamos, encolhemos, curvamos ou deformamos (sem colá-los nem quebrá-los).
Dados: Características e informação, quase sempre na forma de fatos e aspectos quantitativos, coletados por meio de observações ou de outros recursos.
Conjunto de dados: Coleção de dados, geralmente numa forma que possa ser estudada com o uso de um computador.
Análise topológica de dados: Conjunto de técnicas para o estudo da “forma” de dados mediante o uso da topologia.
Escala: Tamanho característico de um objeto, como o raio de um disco ou o comprimento do lado de um quadrado.
Referências
[1] Ghrist, R. W. 2014. “Elementary applied topology.” Seattle, WA: Createspace. Disponível online em https://www.math.upenn.edu/~ghrist/notes.html.
[2] Stolz, B. J. e Mahler, B. I. 2015. ‘H’ is for Homology. Disponível online em https://www.maths.ox.ac.uk/about-us/life-oxford-mathematics/oxford-mathematics-alphabet/h-homology.
[3] Otter, N., Porterm, M. A., Tillmann, U., Grindrod, P. e Harrington, H. A. 2017. “A roadmap for the computation of persistent homology.” EPJ Data Sci. 6:17. DOI: 10.1140/epjds/s13688-017-0109-5.
[4] SIAM News. 2020. January/February 2020 Issue. SIAM. 53. Disponível online em https://sinews.siam.org/Current-Issue/Issue-Archives/Issue-Archives-ListView/PID/2282/mcat/2279/evl/0/TagID/302?TagName=Volume-53-│-Number-1-│-January%FFebruary-2020.
[5] Topaz, C. M. 2016. Topological data analysis: one applied mathematician’s heartwarming story of struggle, triumph, and (ultimately) more struggle. DSWeb: The Dynamical Systems Web. Disponível online em https://dsweb.siam.org/The-Magazine/Article/topological-data-analysis.
[6] Cisewski-Kehe, J., Wu, M., Fasy, B., Hellwing, W., Lovell, M., Rinaldo, A. et al. 2018. “Investigating the cosmic web with topological data analysis”, em American Astronomical Society Meeting Abstracts #231. Washington, DC. Disponível online em https://ui.adsabs.harvard.edu/abs/2018AAS…23121307C/abstract.
[7] Ronellenfitsch, H., Lasser, J., Daly, D. C. e Katifori, E. 2015. “Topological phenotypes constitute a new dimension in the phenotypic space of leaf venation networks.” PLoS Comput. Biol. 11:e1004680. DOI: 10.1371/journal.pcbi.1004680.
[8] ↑ Feng, M. e Porter, M. A. 2021. “Persistent homology of geospatial data: a case study with voting.” SIAM Rev. 63:67–99. DOI: 10.1137/19M1241519.
[9] ↑ Topaz, C. M., Zeigelmeier, L. e Halverson, T. 2015. “Topological data analysis of biological aggregation models.” PLoS ONE 10:e0126383. DOI: 10.1371/journal.pone.0126383.
Citação
Feng, M., Hickok, A., Kureh, Y., Porter, M. e Topaz, C. (2021). “Connecting the dots: discovering the ‘shape’ of data.” Front. Young Minds. 9:551557. DOI: 10.3389/frym.2021.551557.
Este é um artigo de acesso aberto distribuído sob os termos da Creative Commons Attribution License (CC BY). O uso, distribuição ou reprodução em outros fóruns é permitido, desde que o(s) autor(es) original(is) e o(s) proprietário(s) dos direitos autorais sejam creditados e que a publicação original nesta revista seja citada, de acordo com a prática acadêmica aceita. Não é permitido nenhum uso, distribuição ou reprodução que não esteja em conformidade com estes termos.
Encontrou alguma informação errada neste texto?
Entre em contato conosco pelo e-mail:
parajovens@unesp.br


